题目内容
【题目】解比例。
∶
＝x∶9 
∶
＝
∶x
36∶x＝54∶3 
∶
＝∶x
【答案】x＝0.4；x＝
；x＝
；
x＝4.2；x＝2；x＝
【解析】
（1）根据比例的基本性质，将
进行交叉相乘，原式变为75x＝1.2×25，然后等号左右两边同时除以75即可解答；
（2）根据比例的基本性质，将
∶
＝x∶9变为x＝×9，然后等号左右两边同时乘以
即可解答；
（3）根据比例的基本性质，将
∶
＝
∶x变为x＝×，然后等号左右两边同时乘以2即可解答；
（4）根据比例的基本性质，将
进行交叉相乘，原式变为0.4x＝0.7×2.4，然后等号左右两边同时除以0.4即可解答；
（5）根据比例的基本性质，将36∶x＝54∶3变为54x＝36×3，然后等号左右两边同时除以54即可解答；
（6）根据比例的基本性质，将
∶
＝∶x变为x＝×，然后等号左右两边同时乘以6即可解答。
解：75x＝1.2×25
75x＝30
x＝0.4
∶＝x∶9
解：x＝×9
x＝6
x＝6×
x＝
∶＝∶x
解：x＝×
x＝
x＝×2
x＝
解：0.4x＝0.7×2.4
0.4x＝1.68
x＝1.68÷0.4
x＝4.2
36∶x＝54∶3
解：54x＝36×3
54x＝108
x＝2
∶＝∶x
解：x＝×
x＝
x＝×6
x＝
名校课堂系列答案【题目】以中心广场为观测点，量一量，算一算，填写下表。
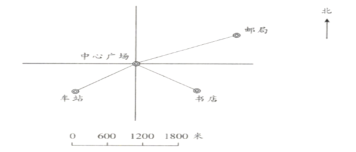
地点 | 方向 | 图上距离/厘米 | 实际距离/米 |
车站 | （______）偏（______）（______） | （______） | （______） |
书店 | （______）偏（______）（______） | （______） | （______） |
邮局 | （______）偏（______）（______） | （______） | （______） |
【题目】推导“圆锥的体积计算公式”时，小明做了几次实验，实验情况见下表：
圆柱与圆锥 | 等底等高 | 等底不等高 | 等高不等底 | 不等底不等高 |
几次倒满 | 3次 | 3.5次、4次、2.5次 | 2次、3次、5次 | 2次、4次 |
在观察表后，小明总结说：“圆锥的体积等于和它等底等高的圆柱体积的三分之一，其它的圆柱与圆锥不可能存在这种关系．”你认为小明说的对吗？为什么一定要用等底等高的圆柱来推导圆锥的体积？