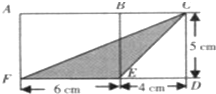
题目内容
4.A,B,C三个桶中各装有一些水,先将A桶中水的$\frac{1}{3}$倒给B桶,再将B桶里水的$\frac{1}{5}$倒入C桶,最后再将C桶水的$\frac{1}{7}$倒回A桶,这时,三个桶中的水都是12升,问原来三个桶各有水多少升?分析 由于将最后再将C桶水的$\frac{1}{7}$倒回A桶同,则此时C根内还剩下倒出前的1-$\frac{1}{7}$=$\frac{6}{7}$,所以C桶在倒出前是12$÷\frac{6}{7}$=14升,又由于再将B桶里水的$\frac{1}{5}$倒入C桶后,B桶有12升,则此时B桶还剩下倒出前的1-$\frac{1}{5}$=$\frac{4}{5}$,所以B桶倒出前是12÷$\frac{4}{5}$=15升,则倒给了C桶15×$\frac{1}{5}$=3升,所以C桶原有14-3=11升,由于此时也A有12升,所以A倒出$\frac{1}{3}$后还剩下12-14×$\frac{1}{7}$=10升,又A原来剩下全部的1-$\frac{1}{3}$,所以A原有10÷(1-$\frac{1}{3}$)=15升,所以B桶原有15-15×$\frac{1}{3}$=10升.
解答 解:12÷(1-$\frac{1}{7}$)
=12÷$\frac{6}{7}$
=14(升)
12÷(1-$\frac{1}{5}$)
=12$÷\frac{4}{5}$
=15(升)
14-15×$\frac{1}{5}$
=14-3
=11(升)
(12-14×$\frac{1}{7}$)÷(1-$\frac{1}{3}$)
=10$÷\frac{2}{3}$
=15(升)
15-15×$\frac{1}{3}$
=15-5
=10(升)
答:A原有15升,B原有10升,C原有11升.
点评 完成本题要注意分析所给条件,然后通过倒推法逐步推出.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目