题目内容
19.计算如图所示的图形的面积.(单位:厘米).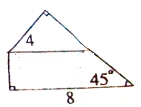
分析 
如上图,延长CB和DA相交于F点,因为三角形CDF是直角三角形,∠D=45°,所以CF=CD=8,利用底×高÷2求三角形CDF的面积,8×8÷2=32,三角形ABF也是直角三角形,所以AB=AF=4,三角形ABF的面积是:4×4÷2=8,再用三角形CDF的面积减去三角形ABF的面积就是所求图形的面积.
解答 
解:如上图,三角形CDF的面积是:8×8÷2=32(平方厘米)
三角形ABF的面积是:4×4÷2=8(平方厘米)
所求图形的面积是:32-8=24(平方厘米)
答:所求图形的面积是24平方厘米.
故答案为:24平方厘米.
点评 这道题是考查利用直角三角形的特征和面积公式来解决,要仔细分析图形,把不规则的图形变成规则的图形,利用规则图形的面积进行计算.

练习册系列答案
相关题目
9.递等式计算:
| 18×$\frac{5}{27}$ | $\frac{1}{6}$+$\frac{3}{4}$+$\frac{3}{8}$ | 7-$\frac{4}{15}$-$\frac{11}{15}$ |
| $\frac{5}{8}$÷$\frac{2}{7}$ | $\frac{18}{25}$×$\frac{5}{9}$ | 1-($\frac{3}{10}$+$\frac{3}{5}$) |
9.下面各题,怎样算简便就怎样算
| $\frac{1}{5}$+$\frac{5}{6}$+$\frac{4}{5}$ | $\frac{1}{6}$+$\frac{1}{2}$-$\frac{1}{6}$ | $\frac{4}{5}$-$\frac{3}{10}$+$\frac{1}{3}$ |
| 1-$\frac{1}{5}$-$\frac{3}{5}$ | $\frac{1}{15}$+$\frac{6}{13}$+$\frac{7}{13}$+$\frac{14}{15}$ | $\frac{7}{12}$+$\frac{11}{18}$-$\frac{7}{12}$ |