题目内容
数1,2,3,4,…,10000按下列方式排列:
1 2 3 …100
101 102 103 …200
…
9901 9902 9903 …10000
任取其中一数,并划去该数所在的行与列.这样做了100次以后,求所取出的100个数的和.
1 2 3 …100
101 102 103 …200
…
9901 9902 9903 …10000
任取其中一数,并划去该数所在的行与列.这样做了100次以后,求所取出的100个数的和.
分析:任取其中一数,并划去该数所在的行与列.做了100次,那么在这个100行100列的排列中,这100个数一定是不同行,不同列,同时也说明每一行、每一列中都有一个数,那么求所取出的100个数的和时,就可以取一种特殊情况,即此数列的对角线上的数:1,102,203,304,405,506,…9798,9899,10000; 是一个后一个数比前一个数大101的数列,共100个数.按照高斯求1+2+3+…+100的方法可得解,即:第一个数+最后一个数=第二个数+倒数第二个数=…=第50个数+第51个数,共50对,利用乘法可求解.
解答:解:1+102+203+304+405+…+9798+9899+10000
=(1+10000)×50
=10001×50
=500050;
所取出的100个数的和是500050.
=(1+10000)×50
=10001×50
=500050;
所取出的100个数的和是500050.
点评:此题考查了数列中的规律,关键按照题意找出一个特殊的数列,来求解.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
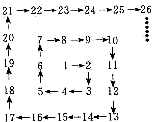 数1,2,3,4,…按箭头所指方向顺序排列(如图),依次在2,3,5,7,10,…等数的位置处拐弯.
数1,2,3,4,…按箭头所指方向顺序排列(如图),依次在2,3,5,7,10,…等数的位置处拐弯.