题目内容

如图的图1和图2，（　　）选项正确．
 
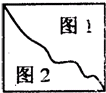
分析：观察图形可知，图形图1的周长，等于长方形的周长的一半与中间曲线的和，图形图2的周长也等于长方形的周长的一半与中间曲线的和，所以这两个图形的周长相等，据此即可解答．
解答：解：根据题干分析可得图形图1与图形图2的周长都等于长方形的周长的一半与中间曲线的和，
所以它们的周长相等．
故选：A．
点评：此题主要考查了周长的定义及长方形的特征，注意中间的虽然是曲线，但计算周长时也要算入．
练习册系列答案
相关题目
（2009?镇江）在如图的方格纸上

（1）画出图①的另一半，使它成为一个轴对称图形．
（2）把图②绕O点逆时针旋转90°，画出旋转后的图形．旋转后M点的位置用数对表示是（
3
3
：
23
23
）．
（3）按2：1的比画出图③放大后的图形．放大后的正方形和原来正方形的面积比是（
4
4
：
1
1
）．
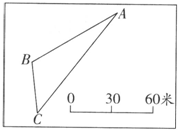（2013?海淀区模拟）操作计算．
（1）根据如图完成下列各题．
①把线段比例尺改成数值比例尺是
1：3000
1：3000
．
②量得AC的长是
3
3
厘米，AC的实际长度是
90
90
米．
③量得∠B=
110
110
度．（精确到十位）
④画出从B点到AC边的最短路线．
⑤求出△ABC的图上面积是
1.5
1.5
平方厘米．
（2）自学下面这段材料，然后回答问题．
我们知道，在整数中“两个数的和等于这两个数的积”的情形并不多，例如2+2=2×2．但是在分数中，这种现象却很普遍．请观察下面的几个例子：
因为：
7
4
+
7
3
=4
1
12
，
7
4
×
7
3
=4
1
12
，所以
7
4
+
7
3
=
7
4
×
7
3
．
因为：
9
5
+
9
4
=4
1
20
，
9
5
×
9
4
=4
1
20
，所以
9
5
+
9
4
=
9
5
×
9
4
．
根据以上结果，我们发现了这样的一个规律：两个分数，如果它们的
分子
分子
相同，并且
分母相差1
分母相差1
，那么这两个分数的和等于它们的积．例如
5
3
5
3
+
5
4
5
4
=
5
3
5
3
×
5
4
5
4
．
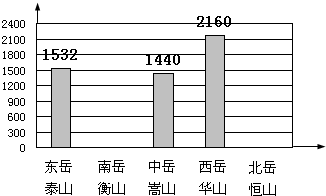精英家教网如图的条形图表示我国五岳的高度．
（1）南岳衡山1290米、北岳恒山2017米，在条形图里画出表示它们高度的直条．
（2）五岳中
 
最高，泰山和
 
的高度比较接近．

阅读下列材料，并解决后面的问题．
★阅读材料：
我国是历史上较早发现并运用“勾股定理”的国家之一．我中古代把直角三角形中较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”，“勾股定理”因此而得名．
勾股定理：如果直角三角形两直角边长分别为a，b，斜边长为c，那么a2+b2=c2．即直角三角形两直角边的平方和等于斜边的平方．请运用“勾股定理”解决以下问题：

（1）如图一，分别以直角三角形的边为边长作正方形，其中s1=400，s2=225，则s3=________．
（2）如图二，是一个园柱形饮料罐，底面半径=8，高=15，顶面正中有一个小园孔，则一条直达底部的直吸管的最大长度是________．注：罐壁厚度和顶部园孔直径忽略不计．
（3）如图三，所示的直角三角形中，AB=6．则s1+s2的值=________． 注π值取3．
（4）如图四的圆柱，高=5厘米，底面半径=4厘米，在园柱底面A点有一只蚂蚁，它想吃到与A点相对的B点处的食物，需要爬行的路程是多少？小聪是这样思考的：
①将该园柱的侧面展开后得到一个长方形，如图五所示（A点的位置已经给出），请在图中中标出B点的位置并连接AB．
②小聪认为线段AB的长度是蚂蚁爬行的最短路程，那么蚂蚁爬行的最短路程是________厘米．注：π值取3．
（5）如图六，在长方形的底面A点有一只蚂蚁，想吃到上底面与A点相对的B点处的食物，它沿长方形表面爬行的最短路程是________厘米．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网