Question

（2008?金坛市）如果用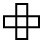去框右面这个数表里的数，每次框出5个数，一共可以框出

15

个不同的和．如果框出的5个数的和是130，这个5个数中最小的一个是

19

．

1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30	31	32	33	34	35

Answer 1

分析：通过观察可知，此数表行5列7，此“十”字框横竖各三个空，则：（1）横着看，第一行至第三行一共有5种不同的框法，由于这些数自左向右都是逐渐增大的，所以就会框出5种不同的和；竖着看，第一列至第三列一共有3种不同的框法，由于这些数自上向下都是逐渐增大的，所以就会框出3种不同的和；再用6乘4就是框出不同和的个数即5×3=15个不同的和．
（2）从表格可看出框的5个数，左右与中间相差1，上下与中间相差7，设中间的数是x，左边的就为x-1，右边的为x+1，下面的就为x+7，上边的为x-7；再由它们的和是130列出方程求解．

解答：解：（1）由于横着看第一行至第三行一共有5种不同的框法，
竖着看，第一列至第三列一共有3种不同的框法，
根据乘法原理可知，共可框出5×3=15种不同的和．
（2）设中间的数是x，左边的就为x-1，右边的为x+1，下面的就为x+7，上边的为x-7，
由此可得方程：
x+x+1+x-1+x+7+x-7=130
               5x=130，
                x=26．
则这五个数中最小的是26-7=19．
故答案为：15，19．

点评：完成此类问题可实际操作一下，找出规律后再进行分析解答．