题目内容
13.甲、乙两仓库共存粮950吨,如果从甲仓库取出$\frac{1}{4}$放入乙仓库,这时乙仓库存粮的$\frac{3}{5}$正好是甲仓库存粮的$\frac{2}{3}$,甲、乙仓库原来各存粮多少吨?分析 设甲仓库原来存粮x吨,则乙仓库原来存粮950-x吨,根据等量关系:甲仓库存粮×(1-$\frac{1}{4}$)×$\frac{2}{3}$=(乙仓库原来存粮+甲仓库原来存粮×$\frac{1}{4}$)×$\frac{3}{5}$,列方程解答即可得甲仓库原来存粮的吨数,再求乙仓库原来存粮即可.
解答 解:设甲仓库原来存粮x吨,则乙仓库原来存粮950-x吨,
(1-$\frac{1}{4}$)×$\frac{2}{3}$x=(950-x+$\frac{1}{4}$x)×$\frac{3}{5}$
$\frac{1}{2}$x=(950-$\frac{3}{4}$x)×$\frac{3}{5}$
$\frac{1}{2}$x=570-$\frac{9}{20}$x
$\frac{19}{20}$x=570
x=600
950-600=350(吨)
答:甲仓库原来存粮600吨、乙仓库原来存粮350吨.
点评 本题考查了分数四则复合应用题,关键是根据等量关系:甲仓库存粮×(1-$\frac{1}{4}$)×$\frac{2}{3}$=(乙仓库原来存粮+甲仓库原来存粮×$\frac{1}{4}$)×$\frac{3}{5}$,列方程.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
3.看线段图,写出等量关系式并列出方程,不求解
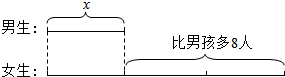

| 等量关系 | 方程 |
| 女生人数-男生人数=8 | 3x-x=8 |
| 女生人数=男生人数+8 | 3x=x+8 |
7.在曹甸镇街道平面图上,小乐的位置是(4,8),小海的家的位置是(4,9).在这个图上,两个人在
( )
( )
| A. | 同一列 | B. | 同一行 | ||
| C. | 既不在同一列,又不在同一行 |