题目内容
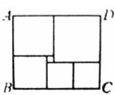 如图所示,矩形ABCD被分割成6个正方形,其中最小正方形的边长等于a,矩形ABCD的面积等于572,则a=
如图所示,矩形ABCD被分割成6个正方形,其中最小正方形的边长等于a,矩形ABCD的面积等于572,则a=2
2
.分析:可设右下角的正方形的边长为未知数,表示出其余正方形的边长,根据最大正方形边长的两种表示方法相等可得未知数的值,进而得到矩形的边长,根据矩形ABCD的面积等于572列方程求解.
解答:解:设右下角的正方形的边长为x.
AB=x+a+(x+2a)=2x+3a,BC=2x+(x+a)=3x+a,
最大正方形可表示为2x-a,也可表示为x+3a,
2x-a=x+3a,
解得x=4a,
则AB=11a,BC=13a,
矩形的面积为11a×13a=572,
a2=4,
所以a=2;
故答案为:2.
AB=x+a+(x+2a)=2x+3a,BC=2x+(x+a)=3x+a,
最大正方形可表示为2x-a,也可表示为x+3a,
2x-a=x+3a,
解得x=4a,
则AB=11a,BC=13a,
矩形的面积为11a×13a=572,
a2=4,
所以a=2;
故答案为:2.
点评:考查长方形、正方形的面积和一元一次方程的应用;得到最大正方形的两种表达形式是解决本题的突破点.

练习册系列答案
相关题目
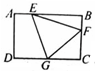 如图所示,矩形ABCD的面积为48,E是AB的四等分点,F是BC的三等分点,G是CD的中点,则三角形EFG的面积是
如图所示,矩形ABCD的面积为48,E是AB的四等分点,F是BC的三等分点,G是CD的中点,则三角形EFG的面积是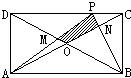 (2012?武汉模拟)如图所示,矩形ABCD的面积为24平方厘米.三角形ADM与三角形BCN的面积之和为7.8平方厘米,则四边形PMON的面积是
(2012?武汉模拟)如图所示,矩形ABCD的面积为24平方厘米.三角形ADM与三角形BCN的面积之和为7.8平方厘米,则四边形PMON的面积是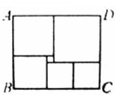 如图所示,矩形ABCD被分割成6个正方形,其中最小正方形的边长等于a,矩形ABCD的面积等于572,则a=________.
如图所示,矩形ABCD被分割成6个正方形,其中最小正方形的边长等于a,矩形ABCD的面积等于572,则a=________.