题目内容
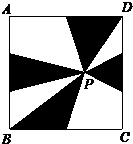 在边长为6厘米的正方形ABCD内任取一点P,将正方形的一组对边二等分,另一组对边三等分,分别与P点连接,求阴影部分面积.
在边长为6厘米的正方形ABCD内任取一点P,将正方形的一组对边二等分,另一组对边三等分,分别与P点连接,求阴影部分面积.分析:如图,△PDA与△PBC的面积等于正方形ABCD面积的
,这两个三角形中的阴影部分又分别是这两个三形面积的
,这两个阴影之和是正方形面积的
;同理,△PAB与△PCD的面积等于正方形ABCD面积的
,这两个三角形中的阴影部分又分别是这两个三形面积的
,这两个阴影之和是正方形面积的
.据此即可求出求阴影部分面积.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
解答:解:如图,连结PA、PC,

△PDA与△PBC的面积等于正方形ABCD面积的
,
这两个三角形中的阴影部分又分别是这两个三形面积的
,
因此,这两个阴影之和是正方形ABCD面积的
;
同理,△PAB与△PCD的面积等于正方形ABCD面积的
,
这两个三角形中的阴影部分又分别是这两个三形面积的
,
因此,这两个阴影之和是正方形ABCD面积的
;
所以,阴影部分面积:6×6×(
+
)
=6×6×
=15(平方厘米)
答:阴影部分面积是15平方厘米.
故答案为:15平方厘米.

△PDA与△PBC的面积等于正方形ABCD面积的
| 1 |
| 2 |
这两个三角形中的阴影部分又分别是这两个三形面积的
| 1 |
| 2 |
因此,这两个阴影之和是正方形ABCD面积的
| 1 |
| 4 |
同理,△PAB与△PCD的面积等于正方形ABCD面积的
| 1 |
| 2 |
这两个三角形中的阴影部分又分别是这两个三形面积的
| 1 |
| 3 |
因此,这两个阴影之和是正方形ABCD面积的
| 1 |
| 6 |
所以,阴影部分面积:6×6×(
| 1 |
| 4 |
| 1 |
| 6 |
=6×6×
| 5 |
| 12 |
=15(平方厘米)
答:阴影部分面积是15平方厘米.
故答案为:15平方厘米.
点评:关键是连结PA、PC,把正方形分成上、下、左、右四个三角形,由于上、下两个阴影是以正方形的边长的一半为底的三角形,它们高之和是正方形的边长,因此,这两个阴影面积之和是正方形面积的
的
,同理中,左、右两边的两个阴影面积之和是正方形面积
的
,从而求出阴影部分的面积.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |

练习册系列答案
相关题目
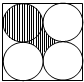 如图,在边长为6厘米的正方形内,有四个半径相等的圆,每相邻的两个圆仅有一个公共点,求阴影部分的面积为
如图,在边长为6厘米的正方形内,有四个半径相等的圆,每相邻的两个圆仅有一个公共点,求阴影部分的面积为
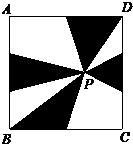 在边长为6厘米的正方形ABCD内任取一点P,将正方形的一组对边二等分,另一组对边三等分,分别与P点连接,求阴影部分面积.
在边长为6厘米的正方形ABCD内任取一点P,将正方形的一组对边二等分,另一组对边三等分,分别与P点连接,求阴影部分面积.