题目内容
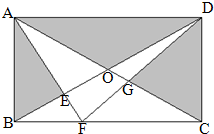在长方形ABCD中，AD=15厘米，AB=8厘米，四边形EFGO的面积是9平方厘米，阴影部分的面积是多少平方厘米？
解：15×8-15×8÷2+9，
=120-60+9，
=69（平方厘米）．
答：阴影部分的面积是69平方厘米．
分析：由图示得：其中△DBF和△AFC是等高的三角形，所以2个三角形面积和=（BF+CF）×AB÷2=BC×AB÷2，又因为四边形EFGO在两个三角形中，重复减了两次，要再加上一次，阴影部分面积=长方形ABCD的面积-（△DBF的面积+△AFC的面积）+9．
点评：解决本题的关键是找到关系式：阴影部分面积=长方形ABCD的面积-（△DBF的面积+△AFC的面积）+9．
=120-60+9，
=69（平方厘米）．
答：阴影部分的面积是69平方厘米．
分析：由图示得：其中△DBF和△AFC是等高的三角形，所以2个三角形面积和=（BF+CF）×AB÷2=BC×AB÷2，又因为四边形EFGO在两个三角形中，重复减了两次，要再加上一次，阴影部分面积=长方形ABCD的面积-（△DBF的面积+△AFC的面积）+9．
点评：解决本题的关键是找到关系式：阴影部分面积=长方形ABCD的面积-（△DBF的面积+△AFC的面积）+9．
练习册系列答案
相关题目
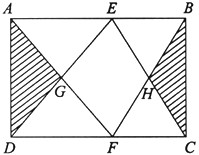如图，在长方形ABCD中，AE=DF，已知阴影部分的面积是16cm2，四边形EGFH的面积是
在长方形ABCD中，AB=120厘米，点Q以每秒3厘米的速度从A向B运动，点P以每秒4厘米的速度从C向D运动，两点同时运动多少秒后，P，Q的连线将长方形ABCD的面积分成3：5两部分？
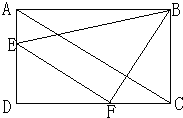[“神奇‘的辅助线]．在长方形ABCD中，EF平行AC，如果△BFC的面积是30平方厘米，那么△AEB的面积是多少平方厘米？
如图，在长方形ABCD中，以AB为轴旋转一周所形成的图形是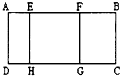
如图，在长方形ABCD中，EFGH是正方形．如果AF=16厘米，HC=21厘米，那么长方形ABCD的周长是