题目内容
19．
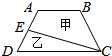如图ABCD是一个梯形，E是AD的中点，直线CE把梯形分成甲、乙两部分，其面积之比是15：7，问上底AB与下底CD的长度之比是（ ）| A． | 5：7 | B． | 6：7 | C． | 4：7 | D． | 3：7 |
分析 如图，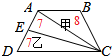
连接AC，把图形ABCE分成两部分，三角形ABC和三角形ACE，因为E是AD的中点，三角形ACE和三角形DCE的面积相等，根据题意把三角形DCE的面积看作7份，图形ABCE的面积看作15份，三角形ACE的面积也是7份，三角形ABC的面积是15-7=8份，三角形ACD的面积是7+7=14份，三角形ABC和三角形ACD的高相等，它们面积比就是它们底边的比．
解答 解：连接AC，由分析可得，15-7=8，
8：（7+7）
=8：14
=4：7．
答：上底AB与下底CD的长度之比是4：7．
故选：C．
点评 本题可以用份数思考比较容易，关键是连接AC，表示出三角形ABC和三角形ACD的面积份数，再根据等高的两个三角形，它们底边的比就是它们面积的比．
练习册系列答案
相关题目