题目内容
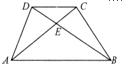
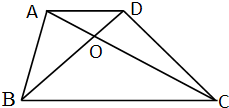 梯形ABCD的上底AD长3厘米,下底BC长9厘米,三角形AOB的面积为18平方厘米,梯形ABCD面积________平方厘米.
梯形ABCD的上底AD长3厘米,下底BC长9厘米,三角形AOB的面积为18平方厘米,梯形ABCD面积________平方厘米.
96
分析:由题意可知:三角形ABD以梯形的上底AD为底与三角形BDC以梯形的下底BC为底时,两个三角形的高相等.说明三角形的高一定,它的面积和三角形的底成正比例关系.再根据两个等底的三角形,它们的面积比等于它们对应高的比;求出△ABC的面积,进而求出△ABC的高(即梯形的高),然后根据梯形的面积公式解答.
解答:三角形ABD以梯形的上底AD为底与三角形BDC以梯形的下底BC为底时,两个三角形的高相等.说明三角形的高一定,它的面积和三角形的底成正比例关系,推出:
OA:OC=3:9=1:3;
三角形AOB与三角形BOC等高,
S△AOB:S△BOC=OA:OC=1:3,
所以S△BOC=3×18=54(平方厘米);
S△ABC=18+54=72(平方厘米);
已知△ABC的面积求出△ABC的高(即梯形的高);
72×2÷9=16(厘米);
梯形的面积:
(3+9)×16× ,
,
=12×16× ,
,
=96(平方厘米).
答:梯形ABCD的面积是96平方厘米.
故答案为:96.
点评:解答此题主要根据:高相等的两个三角形,它们的面积比等于它们对应的底边长的比.底边相等的两个三角形,它们的面积比等于它们对应的高的比.
分析:由题意可知:三角形ABD以梯形的上底AD为底与三角形BDC以梯形的下底BC为底时,两个三角形的高相等.说明三角形的高一定,它的面积和三角形的底成正比例关系.再根据两个等底的三角形,它们的面积比等于它们对应高的比;求出△ABC的面积,进而求出△ABC的高(即梯形的高),然后根据梯形的面积公式解答.
解答:三角形ABD以梯形的上底AD为底与三角形BDC以梯形的下底BC为底时,两个三角形的高相等.说明三角形的高一定,它的面积和三角形的底成正比例关系,推出:
OA:OC=3:9=1:3;
三角形AOB与三角形BOC等高,
S△AOB:S△BOC=OA:OC=1:3,
所以S△BOC=3×18=54(平方厘米);
S△ABC=18+54=72(平方厘米);
已知△ABC的面积求出△ABC的高(即梯形的高);
72×2÷9=16(厘米);
梯形的面积:
(3+9)×16×
 ,
,=12×16×
 ,
,=96(平方厘米).
答:梯形ABCD的面积是96平方厘米.
故答案为:96.
点评:解答此题主要根据:高相等的两个三角形,它们的面积比等于它们对应的底边长的比.底边相等的两个三角形,它们的面积比等于它们对应的高的比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
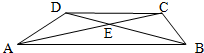 如图,在梯形ABCD中,CD,AB分别是梯形的上底和下底,AC与BD交于点E,并设三角形ADE的面积是S1,三角形BCE的面积是S2,则( )
如图,在梯形ABCD中,CD,AB分别是梯形的上底和下底,AC与BD交于点E,并设三角形ADE的面积是S1,三角形BCE的面积是S2,则( )
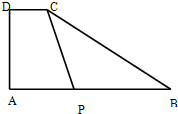
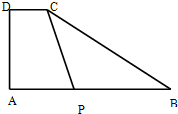 四边形ABCD是一个直角梯形,角A等于90度,它的上底DC=2厘米,DA=5厘米,AB=10厘米.如果三角形PBC的面积等于梯形APCD的面积,那么PB=
四边形ABCD是一个直角梯形,角A等于90度,它的上底DC=2厘米,DA=5厘米,AB=10厘米.如果三角形PBC的面积等于梯形APCD的面积,那么PB=