题目内容
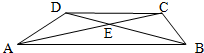 如图,在梯形ABCD中,CD,AB分别是梯形的上底和下底,AC与BD交于点E,并设三角形ADE的面积是S1,三角形BCE的面积是S2,则( )
如图,在梯形ABCD中,CD,AB分别是梯形的上底和下底,AC与BD交于点E,并设三角形ADE的面积是S1,三角形BCE的面积是S2,则( )分析:根据同底等高判断△ABC和△ADB的面积相等,然后都减去△ABE,即可判断.
解答:解:在梯形ABCD中,△ABC和△DBC同底等高面积相等,
同时减去△ABE,△ABC-△ABE=△ADB-△ABE,
所以:△AED=△BEC,即是S1=S2.
故选:C.
同时减去△ABE,△ABC-△ABE=△ADB-△ABE,
所以:△AED=△BEC,即是S1=S2.
故选:C.
点评:本题主要考查三角形面积的等底等高情况的特性,最后做一个差的运算来判断.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
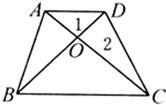 (2010?哈尔滨模拟)如图,在梯形ABCD中,AD与BC平行.已知△AOD的面积是1cm2,△DOC的面积是2cm2,那么梯形ABCD的面积是
(2010?哈尔滨模拟)如图,在梯形ABCD中,AD与BC平行.已知△AOD的面积是1cm2,△DOC的面积是2cm2,那么梯形ABCD的面积是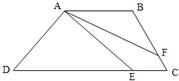 如图,在梯形ABCD中,DE=3EC,BC=3FC,四边形AECF的面积是14平方米,求梯形ABCD的面积是
如图,在梯形ABCD中,DE=3EC,BC=3FC,四边形AECF的面积是14平方米,求梯形ABCD的面积是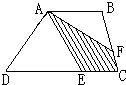 如图,在梯形ABCD中,DC=3EC,BC=3FC,四边形AECF的面积是14平方米.求梯形ABCD的面积是多少平方米?
如图,在梯形ABCD中,DC=3EC,BC=3FC,四边形AECF的面积是14平方米.求梯形ABCD的面积是多少平方米? 如图,在梯形ABCD中,对角线AC、BD相交于O点,OE平行于AB交腰BC于E点,如果三角形OBC的面积是115平方厘米,求三角形ADE的面积?
如图,在梯形ABCD中,对角线AC、BD相交于O点,OE平行于AB交腰BC于E点,如果三角形OBC的面积是115平方厘米,求三角形ADE的面积?