题目内容
 如图,一个长方形被分成A、B、C三块,其中B和C都是长方形,A的八条边的边长分别是1、2、3、4、5、6、7、8厘米.那么B和C的面积和最多是
如图,一个长方形被分成A、B、C三块,其中B和C都是长方形,A的八条边的边长分别是1、2、3、4、5、6、7、8厘米.那么B和C的面积和最多是36
36
平方厘米.(示意图不成比例)分析:根据图和题意,把长方形被分成A、B、C三块的边长分别用小写字母表示出来,然后根据A的八条边的边长进行凑出能满足条件的数,并分别计算出面积,进行比较,从中找出最多有多少平方厘米.
解答:解:由题意知如图,

可知:a=b+c+d,e=f+h-g;
满足第一条等式的有:
6=1+2+3,剩下4、5、7、8,凑出8=5+7-4;
7=1+2+4,剩下3、5、6、8,凑出8=6+5-3;
8=1+2+5,剩下3、4、6、7,凑出7=6+4-3;
8=1+3+4,剩下2、5、6、7,无法凑;
所以长方形长宽有(6、8)(7、8)(8、7)三种情况;
B和C的面积和越大,A的面积越小;
对于于每一种情况在横方向线段长度已经确定的情况下,竖直线段一定是c>b>d的时候A的面积最小;
在竖方向线段长度确定的情况下,横方向一定是f>h的情况面积最小;
依次计算各部分的B和C面积:
1、(3+2)×7-2×4=27(平方厘米);
2、(2+4)×6-2×3=30(平方厘米);
3、(5+2)×6-2×3=36(平方厘米);
所以最多有36平方厘米.
故答案为:36.

可知:a=b+c+d,e=f+h-g;
满足第一条等式的有:
6=1+2+3,剩下4、5、7、8,凑出8=5+7-4;
7=1+2+4,剩下3、5、6、8,凑出8=6+5-3;
8=1+2+5,剩下3、4、6、7,凑出7=6+4-3;
8=1+3+4,剩下2、5、6、7,无法凑;
所以长方形长宽有(6、8)(7、8)(8、7)三种情况;
B和C的面积和越大,A的面积越小;
对于于每一种情况在横方向线段长度已经确定的情况下,竖直线段一定是c>b>d的时候A的面积最小;
在竖方向线段长度确定的情况下,横方向一定是f>h的情况面积最小;
依次计算各部分的B和C面积:
1、(3+2)×7-2×4=27(平方厘米);
2、(2+4)×6-2×3=30(平方厘米);
3、(5+2)×6-2×3=36(平方厘米);
所以最多有36平方厘米.
故答案为:36.
点评:此题考查了组合图形的面积和学生的逻辑思维能力.

练习册系列答案
相关题目
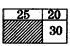
 如图,一个长方形被分A、B、C、D四个长方形,已知A的面积是2平方厘米,B的面积是4平方厘米,C的面积是6平方厘米,求原长方形的面积.
如图,一个长方形被分A、B、C、D四个长方形,已知A的面积是2平方厘米,B的面积是4平方厘米,C的面积是6平方厘米,求原长方形的面积.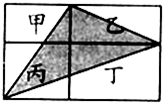 如图,一个长方形被两条互相垂直的线段分割成甲乙丙丁四个小长方形,已知甲、乙、丁的面积分别是12,22,34,那么阴影三角形的面积是
如图,一个长方形被两条互相垂直的线段分割成甲乙丙丁四个小长方形,已知甲、乙、丁的面积分别是12,22,34,那么阴影三角形的面积是 如图,一个长方形被分A、B、C、D四个长方形,已知A的面积是2平方厘米,B的面积是4平方厘米,C的面积是6平方厘米,求原长方形的面积.
如图,一个长方形被分A、B、C、D四个长方形,已知A的面积是2平方厘米,B的面积是4平方厘米,C的面积是6平方厘米,求原长方形的面积.