题目内容
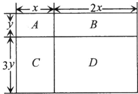
 如图,一个长方形被分A、B、C、D四个长方形,已知A的面积是2平方厘米,B的面积是4平方厘米,C的面积是6平方厘米,求原长方形的面积.
如图,一个长方形被分A、B、C、D四个长方形,已知A的面积是2平方厘米,B的面积是4平方厘米,C的面积是6平方厘米,求原长方形的面积.分析:方法一:在长方形A、B、C的边上标注字母如图,于是原长方形的面积等于(x+2x)×(y+3y)=12xy
因为长方形A的面积等于xy=2平方厘米.
所以原长方形的面积为12xy=12×2=24平方厘米.
方法二:仔细观察图的特征,它的四个长方形是大长方形被两条直线分割后得到的.长方形的面积等于一组邻边的乘积.从横的方向看,两个相邻长方形的倍比关系是一致的,也就是说,B是A的2倍,那么D也是C的2倍,所以D的面积是6×2=12(平方厘米),这样原长方形的面积应是2+4+6+12=24(平方厘米).
因为长方形A的面积等于xy=2平方厘米.
所以原长方形的面积为12xy=12×2=24平方厘米.
方法二:仔细观察图的特征,它的四个长方形是大长方形被两条直线分割后得到的.长方形的面积等于一组邻边的乘积.从横的方向看,两个相邻长方形的倍比关系是一致的,也就是说,B是A的2倍,那么D也是C的2倍,所以D的面积是6×2=12(平方厘米),这样原长方形的面积应是2+4+6+12=24(平方厘米).
解答:解:方法一:如图所示,
原长方形的面积等于(x+2x)×(y+3y)=12xy
因为长方形A的面积等于xy=2平方厘米.
所以原长方形的面积为12xy=12×2=24平方厘米.
方法二:B是A的2倍,那么D也是C的2倍,所以D的面积是6×2=12(平方厘米),
这样原长方形的面积应是2+4+6+12=24(平方厘米).
答:原长方形的面积是24平方厘米.
原长方形的面积等于(x+2x)×(y+3y)=12xy
因为长方形A的面积等于xy=2平方厘米.
所以原长方形的面积为12xy=12×2=24平方厘米.

方法二:B是A的2倍,那么D也是C的2倍,所以D的面积是6×2=12(平方厘米),
这样原长方形的面积应是2+4+6+12=24(平方厘米).
答:原长方形的面积是24平方厘米.
点评:此题难度不大,认真观察图形即其数据特点,灵活的选择的解答方法,问题即可得解.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
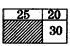
 如图,一个长方形被分成A、B、C三块,其中B和C都是长方形,A的八条边的边长分别是1、2、3、4、5、6、7、8厘米.那么B和C的面积和最多是
如图,一个长方形被分成A、B、C三块,其中B和C都是长方形,A的八条边的边长分别是1、2、3、4、5、6、7、8厘米.那么B和C的面积和最多是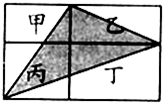 如图,一个长方形被两条互相垂直的线段分割成甲乙丙丁四个小长方形,已知甲、乙、丁的面积分别是12,22,34,那么阴影三角形的面积是
如图,一个长方形被两条互相垂直的线段分割成甲乙丙丁四个小长方形,已知甲、乙、丁的面积分别是12,22,34,那么阴影三角形的面积是 如图,一个长方形被分A、B、C、D四个长方形,已知A的面积是2平方厘米,B的面积是4平方厘米,C的面积是6平方厘米,求原长方形的面积.
如图,一个长方形被分A、B、C、D四个长方形,已知A的面积是2平方厘米,B的面积是4平方厘米,C的面积是6平方厘米,求原长方形的面积.