题目内容
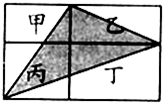 如图,一个长方形被两条互相垂直的线段分割成甲乙丙丁四个小长方形,已知甲、乙、丁的面积分别是12,22,34,那么阴影三角形的面积是
如图,一个长方形被两条互相垂直的线段分割成甲乙丙丁四个小长方形,已知甲、乙、丁的面积分别是12,22,34,那么阴影三角形的面积是34
34
.分析:如下图,连接OB,将阴影部分分成三角形AOB,三角形OBC,三角形AOC三部分;根据等底等高的性质,三角形AOB的面积是甲的面积的一半,三角形0BC的面积是丁的面积的一半,三角形AOC的面积是乙的面积的一半,由此将甲、乙、丁的面积加起来就是阴影部分的面积的2倍,进而得出阴影三角形的面积.
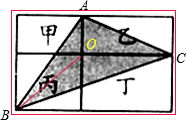

解答:解:(12+22+34)÷2,
=68÷2,
=34,
答:阴影三角形的面积是34;
故答案为:34.
=68÷2,
=34,
答:阴影三角形的面积是34;
故答案为:34.
点评:利用等底等高的性质,得出阴影部分的面积是甲、乙、丁的面积和的一半是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
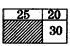
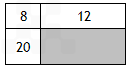
 (2013?郯城县)如图中,长方形被两条直线分成四个小长方形,其中三个的面积分别是12平方米、8平方米、20平方米,求另一个(图中阴影都分)长方形的面积.
(2013?郯城县)如图中,长方形被两条直线分成四个小长方形,其中三个的面积分别是12平方米、8平方米、20平方米,求另一个(图中阴影都分)长方形的面积. 如图,一个长方形被两条互相垂直的线段分割成甲乙丙丁四个小长方形,已知甲、乙、丁的面积分别是12,22,34,那么阴影三角形的面积是________.
如图,一个长方形被两条互相垂直的线段分割成甲乙丙丁四个小长方形,已知甲、乙、丁的面积分别是12,22,34,那么阴影三角形的面积是________.