题目内容
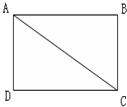 如图所示,四边形ABCD是一个长为4,宽为3,对角线长度为5的长方形.它绕C点接顺时针方向旋转90度,请求出AB边扫过图形的面积.
如图所示,四边形ABCD是一个长为4,宽为3,对角线长度为5的长方形.它绕C点接顺时针方向旋转90度,请求出AB边扫过图形的面积.分析:如下图,在整个AB边上,距离C点最近的点是B点,最远的点是A点,因此整条线段所扫过部分应该介于这两个点所扫过弧线之间,观察图形可以发现,所求阴影部分的面积实际上是:(扇形ACA面积+三角形ABC面积)-(三角形ABC面积+扇形BCB面积),由此解答.
解答:解:如图:

AB边扫过图形的面积就是图中阴影部分的面积,
(扇形ACA面积+三角形ABC面积)-(三角形ABC面积+扇形BCB面积),
=扇形ACA面积-扇形BCB面积,
=3.14×52×
-3.14×32×
,
=3.14×25×
-3.14×9×
,
=3.14×(25-9)×
,
=3.14×16×
,
=12.56(平方单位);
答:AB边扫过图形的面积12.56.

AB边扫过图形的面积就是图中阴影部分的面积,
(扇形ACA面积+三角形ABC面积)-(三角形ABC面积+扇形BCB面积),
=扇形ACA面积-扇形BCB面积,
=3.14×52×
| 1 |
| 4 |
| 1 |
| 4 |
=3.14×25×
| 1 |
| 4 |
| 1 |
| 4 |
=3.14×(25-9)×
| 1 |
| 4 |
=3.14×16×
| 1 |
| 4 |
=12.56(平方单位);
答:AB边扫过图形的面积12.56.
点评:解答此题重点是画图,通过画图很容易看出图中阴影部分的面积就是AB扫过图形的面积,然后再通过转化利用扇形面积的计算方法解决问题.

练习册系列答案
相关题目
 分别延长四边形ABCD的四个边,使得AB=BA′,BC=CB′,CD=DC′,DA=AD′(如图所示).如果四边形ABCD的面积是1平方公分,试求四边形A′B′C′D′的面积?
分别延长四边形ABCD的四个边,使得AB=BA′,BC=CB′,CD=DC′,DA=AD′(如图所示).如果四边形ABCD的面积是1平方公分,试求四边形A′B′C′D′的面积?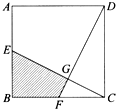 如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是
如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是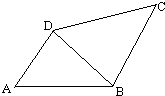 如图所示的四边形ABCD中,∠A=∠C=45°,∠ABC=105°,AB=CD=15厘米,连接对角线BD.求四边形ABCD的面积.
如图所示的四边形ABCD中,∠A=∠C=45°,∠ABC=105°,AB=CD=15厘米,连接对角线BD.求四边形ABCD的面积. 如图所示,四边形ABCD是一个长为4,宽为3,对角线长度为5的长方形.它绕C点接顺时针方向旋转90度,请求出AB边扫过图形的面积.
如图所示,四边形ABCD是一个长为4,宽为3,对角线长度为5的长方形.它绕C点接顺时针方向旋转90度,请求出AB边扫过图形的面积.