题目内容
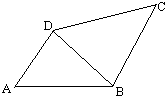 如图所示的四边形ABCD中,∠A=∠C=45°,∠ABC=105°,AB=CD=15厘米,连接对角线BD.求四边形ABCD的面积.
如图所示的四边形ABCD中,∠A=∠C=45°,∠ABC=105°,AB=CD=15厘米,连接对角线BD.求四边形ABCD的面积.分析:将△DCB切下,令DC与AB重合,拼接到△ABD上,得到四边形AEBD.因为∠ABE=∠DCB=45°,所以,BE∥AD,又AE=DB,所以四边形AEBD是等腰梯形.再作AF⊥BE,交BE于F,并将△AEF切下,令AE与BD重合,拼接成四边形AFBD,则AFBD是正方形,它的对角线AB=15厘米,所以这个正方形的面积,再根据对角线互相垂直的对角线互相垂直的四边形的面积是两条对角线的乘积的一半,列式解答即可.
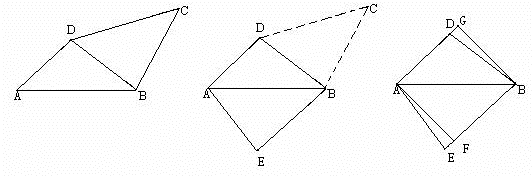

解答:解:如上图所示:
将△DCB切下,令DC与AB重合,拼接到△ABD上,得到四边形AEBD.
因为∠ABE=∠DCB=45°,所以,BE∥AD,又AE=DB,所以四边形AEBD是等腰梯形.
再作AF⊥BE,交BE于F,并将△AEF切下,令AE与BD重合,拼接成四边形AFBD,
则AFBD是正方形,它的对角线AB=15厘米,
所以这个正方形的面积为:(15×15)÷2=112.5(平方厘米).
将△DCB切下,令DC与AB重合,拼接到△ABD上,得到四边形AEBD.
因为∠ABE=∠DCB=45°,所以,BE∥AD,又AE=DB,所以四边形AEBD是等腰梯形.
再作AF⊥BE,交BE于F,并将△AEF切下,令AE与BD重合,拼接成四边形AFBD,
则AFBD是正方形,它的对角线AB=15厘米,
所以这个正方形的面积为:(15×15)÷2=112.5(平方厘米).
点评:本题主要是利用割补的方法,将两个三角形组成一个等腰梯形,进而组成正方形,再利用互相垂直的对角线的乘积的一半是此正方形的面积解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
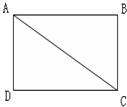 如图所示,四边形ABCD是一个长为4,宽为3,对角线长度为5的长方形.它绕C点接顺时针方向旋转90度,请求出AB边扫过图形的面积.
如图所示,四边形ABCD是一个长为4,宽为3,对角线长度为5的长方形.它绕C点接顺时针方向旋转90度,请求出AB边扫过图形的面积. 分别延长四边形ABCD的四个边,使得AB=BA′,BC=CB′,CD=DC′,DA=AD′(如图所示).如果四边形ABCD的面积是1平方公分,试求四边形A′B′C′D′的面积?
分别延长四边形ABCD的四个边,使得AB=BA′,BC=CB′,CD=DC′,DA=AD′(如图所示).如果四边形ABCD的面积是1平方公分,试求四边形A′B′C′D′的面积? 如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是
如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是 如图所示,四边形ABCD是一个长为4,宽为3,对角线长度为5的长方形.它绕C点接顺时针方向旋转90度,请求出AB边扫过图形的面积.
如图所示,四边形ABCD是一个长为4,宽为3,对角线长度为5的长方形.它绕C点接顺时针方向旋转90度,请求出AB边扫过图形的面积.