题目内容
12.两辆同一型号的汽车从同地同时同速沿一个方向出发,每年最多能带30桶汽油,每桶汽油使汽车前进60千米,每车都须返回出发点,两车可以找对方借油,为了使其中一辆车尽可能远离出发点,那么这辆汽车最远能离出发点多少千米?分析 甲车可以行驶到汽油用掉$\frac{1}{3}$的时候,留$\frac{1}{3}$汽油返程,给另一车加$\frac{1}{3}$汽油,因为此时乙车也刚好用掉汽油的$\frac{1}{3}$,所以乙车实际可用$\frac{4}{3}$的汽油,所以它最远可达60×30÷2×$\frac{4}{3}$千米.据此解答即可.
解答 解:甲车可以行驶到汽油用掉$\frac{1}{3}$的时候,留$\frac{1}{3}$汽油返程,给另一车加$\frac{1}{\;}3$汽油,因为此时乙车也刚好用掉汽油的$\frac{1}{3}$,所以乙车实际可用$\frac{4}{3}$的汽油,乙车可以行驶:
60×30÷2×$\frac{4}{3}$
=1800÷2×$\frac{4}{3}$
=900×$\frac{4}{3}$
=1200(千米)
答:这辆汽车最远能离出发点1200千米.
点评 关键是如何合理分配甲的汽油是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.要形象反映化肥厂2010年下半年每月的产量情况,最好选用( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 以上答案都不对 |
20.冰化成水后,体积减少$\frac{1}{11}$,现有水2立方米,结成冰后体积是( )立方米.
| A. | $\frac{21}{11}$ | B. | $\frac{11}{6}$ | C. | $\frac{11}{5}$ | D. | $\frac{5}{11}$ |
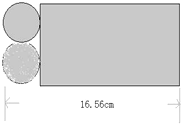 如图,一块长方形铁皮的长是16.56cm,利用图中的阴影部分刚好能做一个圆柱形油桶(接头处不计),求这个油桶的容积?
如图,一块长方形铁皮的长是16.56cm,利用图中的阴影部分刚好能做一个圆柱形油桶(接头处不计),求这个油桶的容积?