题目内容
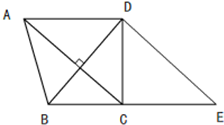 在等腰梯形ABCD中,延长BC到E点,已知线段AC与BD互相垂直,AC与DE互相平行,AD=CE,AD+BC=10厘米,求三角形BDE的面积.
在等腰梯形ABCD中,延长BC到E点,已知线段AC与BD互相垂直,AC与DE互相平行,AD=CE,AD+BC=10厘米,求三角形BDE的面积.
解:过D点作DF⊥BE于F点,
因为DE∥AC,AC⊥BD,
所以DE⊥BD,即∠BDE=90°.
因为AD∥BC,AD=CE,
所以四边形ADCE是平行四边形,
所以DE=AC,CE=AD,
因为四边形ABCD是等腰梯形,
所以AC=DB,
所以DE=DB,
所以△DBE是等腰直角三角形.
所以△DFB也是等腰直角三角形.
所以DF=BF= ×10=5(厘米),
×10=5(厘米),
三角形BDE的面积:10×5÷2=25(平方厘米),
答:三角形BDE的面积是25平方厘米.
分析:如图:过D点作DF⊥BE于F点,平行线间的内错角相等,证明△DBE是直角三角形,再根据四边形ABCD是等腰梯形,证明三角形BDE是等腰直角三角形,由此根据直角三角形斜边上的中线等于斜边的一半,求出DF的值,最后利用三角形的面积公式S=ah÷2,列式解答即可.

点评:证明三角形BDE是等腰直角三角形是解答此题的关键.
因为DE∥AC,AC⊥BD,
所以DE⊥BD,即∠BDE=90°.
因为AD∥BC,AD=CE,
所以四边形ADCE是平行四边形,
所以DE=AC,CE=AD,
因为四边形ABCD是等腰梯形,
所以AC=DB,
所以DE=DB,
所以△DBE是等腰直角三角形.
所以△DFB也是等腰直角三角形.
所以DF=BF=
 ×10=5(厘米),
×10=5(厘米),三角形BDE的面积:10×5÷2=25(平方厘米),
答:三角形BDE的面积是25平方厘米.
分析:如图:过D点作DF⊥BE于F点,平行线间的内错角相等,证明△DBE是直角三角形,再根据四边形ABCD是等腰梯形,证明三角形BDE是等腰直角三角形,由此根据直角三角形斜边上的中线等于斜边的一半,求出DF的值,最后利用三角形的面积公式S=ah÷2,列式解答即可.

点评:证明三角形BDE是等腰直角三角形是解答此题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 在等腰梯形ABCD中,延长BC到E点,已知线段AC与BD互相垂直,AC与DE互相平行,AD=CE,AD+BC=10厘米,求三角形BDE的面积.
在等腰梯形ABCD中,延长BC到E点,已知线段AC与BD互相垂直,AC与DE互相平行,AD=CE,AD+BC=10厘米,求三角形BDE的面积. 在等腰梯形ABCD中,已知它的周长是90厘米,AB长20厘米,CD长40厘米,求AC的长.
在等腰梯形ABCD中,已知它的周长是90厘米,AB长20厘米,CD长40厘米,求AC的长.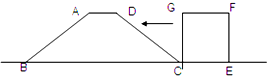 如图,在等腰梯形ABCD中,上底AD=20厘米,下底BC=100厘米,高为40厘米,另有一条边长为40厘米的正方形CEFG沿直线L以每分钟10厘米的速度向左匀速平移(边CE始终在直线L上)当正方形运动到第10分钟时,在图中画出正方形的位置,用阴影表示等腰梯形与正方形的重叠部分,并求出阴影部分的面积.
如图,在等腰梯形ABCD中,上底AD=20厘米,下底BC=100厘米,高为40厘米,另有一条边长为40厘米的正方形CEFG沿直线L以每分钟10厘米的速度向左匀速平移(边CE始终在直线L上)当正方形运动到第10分钟时,在图中画出正方形的位置,用阴影表示等腰梯形与正方形的重叠部分,并求出阴影部分的面积.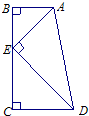 如图,在直角梯形ABCD中,三角形ABE和三角形CDE都是等腰直角三角形,且BC=20厘米,那么直角梯形ABCD的面积是
如图,在直角梯形ABCD中,三角形ABE和三角形CDE都是等腰直角三角形,且BC=20厘米,那么直角梯形ABCD的面积是