题目内容
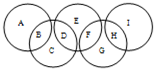 如图,A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,且每个圆中所填数的和都等于2008.这九个数总和最小为
如图,A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,且每个圆中所填数的和都等于2008.这九个数总和最小为5028
5028
.分析:据题意可知,每个圆中所填数的和都等于2008,即(A+C+E+G+I)+2(B+D+F+H)=2008×5,所以当(A+C+E+G+I)最小时,这九个数总和才最小,又A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,所以(A+C+E+G+I)应为偶数,可使A+C+E+G+I=1+2+3+4+6=16,由此就能计算出这个九个数的总和是多少了.
解答:解:(A+C+E+G+I)+2(B+D+F+H)=2008×5,
所以,当A+C+E+G+I=1+2+3+4+6=16时,A+C+E+G+I+B+D+F+H最小.
(1+2+3+4+6)+2(B+D+F+H)=2008×5
16+2(B+D+F+H)=10040;
B+D+F+H=5012;
所以A+C+E+G+I+B+D+F+H=5012+16=5028;
故答案为:5028.
所以,当A+C+E+G+I=1+2+3+4+6=16时,A+C+E+G+I+B+D+F+H最小.
(1+2+3+4+6)+2(B+D+F+H)=2008×5
16+2(B+D+F+H)=10040;
B+D+F+H=5012;
所以A+C+E+G+I+B+D+F+H=5012+16=5028;
故答案为:5028.
点评:完成本题要据已知条件认真分析,找出其中的内在联系来完成.

练习册系列答案
相关题目
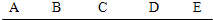 如图,A、B、C、D、E在同一条线上,则图中的 不同的线段共有( )条.
如图,A、B、C、D、E在同一条线上,则图中的 不同的线段共有( )条.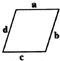 如图,a、b、c、d分别表示平行四边形的四条边,在这四条边中
如图,a、b、c、d分别表示平行四边形的四条边,在这四条边中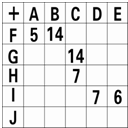 如图,A,B,C,D,E,F,G,H,I,J表示10个各不相同的数字,表中的数为所在行与列的对应字母的和,例如“G+C=14”.请将表中其他的数全部填好.
如图,A,B,C,D,E,F,G,H,I,J表示10个各不相同的数字,表中的数为所在行与列的对应字母的和,例如“G+C=14”.请将表中其他的数全部填好.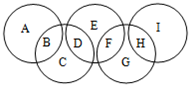 如图,A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,A,B,C,D,E,F,G,H,I的总和为2008,并且每个圆中所填数的和都等于M.
如图,A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,A,B,C,D,E,F,G,H,I的总和为2008,并且每个圆中所填数的和都等于M.