题目内容
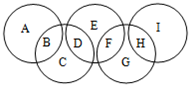 如图,A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,A,B,C,D,E,F,G,H,I的总和为2008,并且每个圆中所填数的和都等于M.
如图,A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,A,B,C,D,E,F,G,H,I的总和为2008,并且每个圆中所填数的和都等于M.(1)M最大为多少?
(2)M最小为多少?
分析:A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,那么M也是正整数,把5个圆中的数加起来进行推算.
解答:解:5个圆中所填数的和为:
(1)2008=(A+B)+C+(D+E+F)+G+(H+I)=3M+C+G,
3M=2008-C-G,要使M大,只需C+G小.
当C+G=1+2时,3M=2008-1-2=2005,但2005不是3的倍数;
当C+G=1+3时,3M=2008-1-3=2004,M=668;
而当A,B,C,D,E,F,G,H,I依次为5,663,1,4,658,6,3,659,9时可使M=668.
答:M最大为668.
(2)A+B+B+C+D+D+E+F+F+H+G+H+I
=2(B+D+F+H)+A+C+E+G+I;
M最小,5M=2008+B+D+F+H;
2008+B+D+F+H是5的倍数,B+D+F+H最小时M最小,
当B+D+F+H=12时,就是取1、2、4、5;
5M=2008+B+D+F+H=2008+12=2020,
M=404;
答:M最小为404.
(1)2008=(A+B)+C+(D+E+F)+G+(H+I)=3M+C+G,
3M=2008-C-G,要使M大,只需C+G小.
当C+G=1+2时,3M=2008-1-2=2005,但2005不是3的倍数;
当C+G=1+3时,3M=2008-1-3=2004,M=668;
而当A,B,C,D,E,F,G,H,I依次为5,663,1,4,658,6,3,659,9时可使M=668.
答:M最大为668.
(2)A+B+B+C+D+D+E+F+F+H+G+H+I
=2(B+D+F+H)+A+C+E+G+I;
M最小,5M=2008+B+D+F+H;
2008+B+D+F+H是5的倍数,B+D+F+H最小时M最小,
当B+D+F+H=12时,就是取1、2、4、5;
5M=2008+B+D+F+H=2008+12=2020,
M=404;
答:M最小为404.
点评:把5个圆中的数加起来,得出与这9个数的和有关的算式,再根据取值情况求解.

练习册系列答案
相关题目
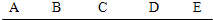 如图,A、B、C、D、E在同一条线上,则图中的 不同的线段共有( )条.
如图,A、B、C、D、E在同一条线上,则图中的 不同的线段共有( )条.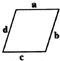 如图,a、b、c、d分别表示平行四边形的四条边,在这四条边中
如图,a、b、c、d分别表示平行四边形的四条边,在这四条边中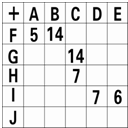 如图,A,B,C,D,E,F,G,H,I,J表示10个各不相同的数字,表中的数为所在行与列的对应字母的和,例如“G+C=14”.请将表中其他的数全部填好.
如图,A,B,C,D,E,F,G,H,I,J表示10个各不相同的数字,表中的数为所在行与列的对应字母的和,例如“G+C=14”.请将表中其他的数全部填好.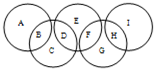 如图,A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,且每个圆中所填数的和都等于2008.这九个数总和最小为
如图,A,B,C,D,E,F,G,H,I代表九个各不相同的正整数,且每个圆中所填数的和都等于2008.这九个数总和最小为