题目内容
2008减去它的 ,再减去第二次余下的
,再减去第二次余下的 ,再减去第二次余下的
,再减去第二次余下的 ,如此下去,一直到第2007次减去2006次余下的
,如此下去,一直到第2007次减去2006次余下的 为止,则最后剩下多少?
为止,则最后剩下多少?
解:2008×(1- )×(1-
)×(1- )×(1-
)×(1- )×…×(1-
)×…×(1-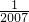 )×(1-
)×(1- ),
),
=2008× ×
× ×
× ×
× ×…×
×…× ×
× ,
,
=2008× ,
,
=1;
答:最后剩下1.
分析:把每一次减去前的数看作单位“1”,每次分别剩:(1- )、(1-
)、(1- )、(1-
)、(1- )、…、(1-
)、…、(1-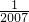 )、(1-
)、(1- );则根据分数乘法的意义可求出最后剩下:2008×(1-
);则根据分数乘法的意义可求出最后剩下:2008×(1- )×(1-
)×(1- )×(1-
)×(1- )×…×(1-
)×…×(1-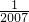 )×(1-
)×(1- );然后利用约分简算即可得出结论.
);然后利用约分简算即可得出结论.
点评:本题重点考查了分数乘法中的巧算,关键是从整体上考虑,利用交叉约分达到速算的目的.
 )×(1-
)×(1- )×(1-
)×(1- )×…×(1-
)×…×(1-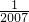 )×(1-
)×(1- ),
),=2008×
 ×
× ×
× ×
× ×…×
×…× ×
× ,
,=2008×
 ,
,=1;
答:最后剩下1.
分析:把每一次减去前的数看作单位“1”,每次分别剩:(1-
 )、(1-
)、(1- )、(1-
)、(1- )、…、(1-
)、…、(1-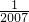 )、(1-
)、(1- );则根据分数乘法的意义可求出最后剩下:2008×(1-
);则根据分数乘法的意义可求出最后剩下:2008×(1- )×(1-
)×(1- )×(1-
)×(1- )×…×(1-
)×…×(1-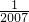 )×(1-
)×(1- );然后利用约分简算即可得出结论.
);然后利用约分简算即可得出结论.点评:本题重点考查了分数乘法中的巧算,关键是从整体上考虑,利用交叉约分达到速算的目的.

练习册系列答案
相关题目
