题目内容
9.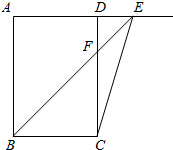 如图长方形ABCD中,E为AD延长线上一点,连接CE、BE,AB=15cm,AD=12cmDE=4cm,△DEF的面积是12cm2.
如图长方形ABCD中,E为AD延长线上一点,连接CE、BE,AB=15cm,AD=12cmDE=4cm,△DEF的面积是12cm2.求:
(1)△CEF的面积.
(2)求梯形ABFD的面积.
分析 (1)观图可知:△CEF的面积=△DEC的面积-△DEF的面积,因为ABCD是长方形,所以AB=DC=15厘米,根据三角形面积公式即可求出△DEC的面积,解决问题;
(2)已知△DEF的面积是12cm2,DE=4cm,运用三角形面积公式可求出DF的长度;又知AB=15cm,AD=12cm,运用梯形面积公式即可解答.
解答 解:(1)4×15÷2-12
=30-12
=18(平方厘米)
答:△CEF的面积是18平方厘米.
(2)DF=12×2÷4=6(厘米)
(6+15)×12÷2
=21×12÷2
=126(平方厘米)
答:梯形ABFD的面积是126平方厘米.
点评 本题是考查求组合图形的面积,此题很容易看出:△CEF的面积=△DEC的面积-△DEF的面积;难度较大的是根据△DEF的面积和DE的长度求出DF的长度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知n是自然数,$\frac{n}{8}$为假分数,$\frac{n}{11}$为真分数,则满足条件的n值有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 重20克,一个
重20克,一个 重20克.
重20克.
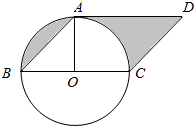 如图,其中平行四边形的面积是80平方厘米,求图中阴影部分的面积.
如图,其中平行四边形的面积是80平方厘米,求图中阴影部分的面积.