Question

11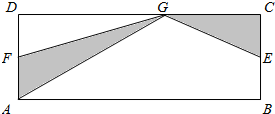．如图，ABCD是一个长方形，AB=20m，AD=5m，E、F分别是BC、AD上的中点，G是线段DC上任意一点，你知道阴影部分面积是多少吗？

Answer 1

分析 根据三角形的面积等于底乘高除以2，用含有字母的式子表示出三角形AFG的面积和三角形CEG的面积，再把这两个面积相加就是阴影部分的面积．

解答 解：阴影部分的面积就是△AFG的面积加△CEG的面积的和．
△AFG的面积=AF×DG×$\frac{1}{2}$
=$\frac{1}{2}$AD×DG×$\frac{1}{2}$
=$\frac{1}{4}$AD×DG，
△CEG的面积=CE×GC×$\frac{1}{2}$
=$\frac{1}{2}$AD×GC×$\frac{1}{2}$
=$\frac{1}{4}$AD×GC，
△AFG的面积+△CEG的面积=$\frac{1}{4}$AD×DG+$\frac{1}{4}$AD×GC
=$\frac{1}{4}$AD×（DG+GC）
=$\frac{1}{4}$×AD×DC
=$\frac{1}{4}$×AD×AB
=$\frac{1}{4}$×5×20
=25（平方米）
答：阴影部分面积是25平方米．

点评 两个阴影部分的三角形的底是长方形宽的一半，高相加是长方形的长，所以阴影部分的面积是长方形宽的一半乘长再除以2．