题目内容
【题目】甲乙两车同时从A地出发,向B地匀速行驶,与此同时,丙车从B地出发向A地匀速行驶,当丙行了30千米时与甲相遇,相遇后甲立即掉头,并且将速度提高到原来的2倍,当甲乙两车相遇时,丙行驶了40千米。当乙丙两车相遇时,甲恰好回到A地,那么AB两地的距离是多少千米?
【答案】54千米
【解析】
此行程问题比较复杂,既有变速问题,又有多次相遇问题。我们可以分开考虑。
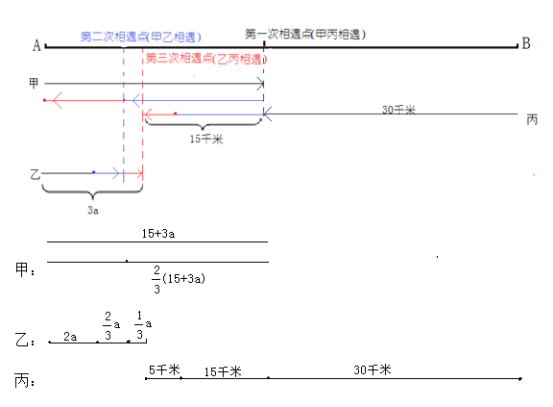
由图可知,甲到达某地又立即2倍速度返回,可以假设甲走了3份时间,因为往返两地总路程不变,速度和时间成反比,返回是去时速度的2倍说明去时用了2份时间,返回用了1份时间;乙的速度没有发生变化,我们可以假设一份时间内乙走的路程是a,可以得出整个行程过程中乙走的路程是3a;再回头考虑丙。根据题意,找出甲乙丙三人的行程与总路程的关系,列方程即可解答。
解:设甲一共走了3份时间,那么从A地到某地用了2份时间,从某地回到A地一共用1份时间;
根据第一次相遇丙行了30千米,可以计算出丙1份时间的路程:30÷2=15千米,丙与乙相遇时丙一共行了30+15=45千米;
乙一份时间路程是a,那么3份时间内,乙走的路程是3a,故AB两地的距离是(3a+45)千米;
甲3份时间内走了从A地到某地路程的2倍,所以甲第一次走的路程是:15+3a;
甲乙两车相遇时,丙又走了40-30=10千米,说明时间用了:10÷15=![]() 份;
份;
那么第二次相遇时,乙一共走的路程是:2a+![]() a,甲从某地返回走的路程是
a,甲从某地返回走的路程是![]() ×(3a+15),两项加起来正好是A地到某地的距离,据此等量关系可列方程:
×(3a+15),两项加起来正好是A地到某地的距离,据此等量关系可列方程:
3a+15=2a+![]() a+
a+![]() ×(3a+15)
×(3a+15)
化简得![]()
解得,![]()
3a+45=3×3+45=54(千米)
答:AB两地的距离是54米。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某商场去年下半年每月羊毛衫的销售情况如下表.
月份 | 七 | 八 | 九 | 十 | 十一 | 十二 |
销售量(件) | 300 | 360 | 600 | 1200 | 800 | 400 |
(1)根据表中的数据完成下面的折线统计图.
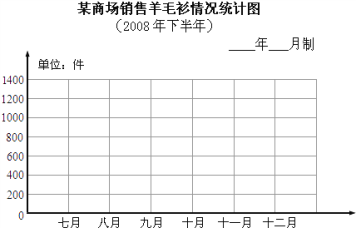
(2)这个商场下半年平均每月销售羊毛衫多少件?
(3)观察、分析上面的统计图,你能提出什么问题,根据你提的问题列式解答.
【题目】为了更好的还房贷,小宇的爸爸决定做一名会挣钱的出租车司机。下面是关于出租车的一些信息,请你来帮忙吧!
需要支出的费用 ①每天固定支出费用=每天需要上交的承包费+每天加气费 ②每个月按30天计算,每天工作12小时。每月需要上交3000元承包费。 ③平均每天的加气费大约是140元。 | 某日2小时营运情况 ①出租车的起步价是2千米8元,单价是每千米1.5元。 ②某日前两个小时营运情况: 第一个1小时里,因为堵车,只拉了一个活儿,打车的路程是14千米。 第二个1小时里,没有堵车,拉了两个活儿.一个路程是10千米,另一个路程是8千米。 |
(1)这辆出租车每天固定支出的费用大约是( )元,每小时固定支出的费用大约是( )元。
(2)在第一个1小时里,爸爸收入了多少钱?净赚了多少钱?(净赚=收入-固定支出)
(3)在第二个1小时里,爸爸净赚了多少钱?
(4)比较两次净赚的钱,你想给爸爸提一些什么建议?
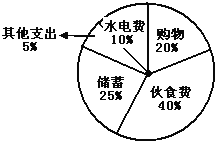
【题目】小明家四月份支出及储蓄情况统计图(如图):
(1)小明家四月份的伙食费共花了800元,小明家的支出及储蓄总共是多少元?
(2)根据扇形统计图,把下表填完整.
项目 | 伙食费 | 购物 | 水电费 | 储蓄 | 其他支出 | 总计 |
费用/元 | 800 | |||||
百分比% | 40% |