题目内容
【题目】有4袋糖块，其中任意3袋的总和都超过60块．那么这4袋糖块的总和最少有多少块?
【答案】82
【解析】方法一：设这4袋为A、B、C、D，为使4袋糖块的总和最少，则每袋糖应尽量平均，有A、B、C袋糖有20、20、21块糖．
则当A、B、D三袋糖在一起时，为了满足条件，D袋糖不少于21块，验证A、B、C、D这4袋糖依次有20，20，2l，2l时满足条件，且总和最少．
这4袋糖的总和为20+20+21+21=82块．
方法二：设这4袋糖依次有a、b、c、d块糖，
有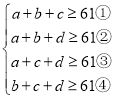
，①+②+③+④得：3（a+b+c+d）≥244,所以a+b+c+d≥81
,因为a+b+c+d均是整数，所以a+b+c+d的和最小是82．
不能把不等式列为
，如果这样将①+②+③+④得到3(a+b+c+d)>240,a+b+c+d>80，因为a、b、c、d均是整数，所以a+b+c+d的和最小是81.
练习册系列答案
阅读快车系列答案
相关题目
