题目内容
【题目】画图并解决下面问题:
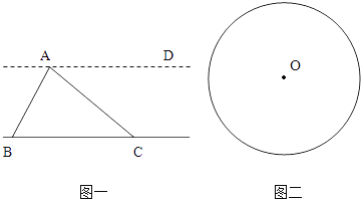
图一:
①画出三角形ABC的BC边上的高.
②根据直线BC与AD平行,不用测量任何数据,在直线BC的右边画一个与三角形ABC面积相等的三角形.
图二:是一个半径2厘米的圆.
①在这个圆内画出一个最大的正方形.
②正方形的面积比圆面积少________平方厘米.
【答案】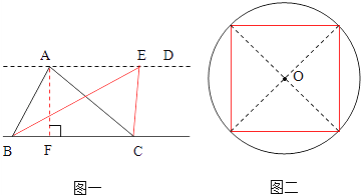 4.56
4.56
【解析】
(1)①按照“过一点作已知直线的垂线”进行作图即可;②因为平行线间的距离处处相等和等底等高的三角形的面积相等的性质,以BC为底,以Z直线AD上任意一点为顶点,即可画出与已知三角形ABC面积相等的三角形;(2)①圆内最大正方形的对角线应等于圆的直径,因此可以画两条互相垂直的直径,依次连接两条直径的4个端点,即可完成作图;②利用正方形的面积可以利用两条对角线的乘积除以2进行计算;再利用圆的面积公式求出圆的面积,再相减即可解答.
(1)此题考查的知识点有:垂线的画法,平行线间的距离处处相等的性质,三角形的面积公式;(2)解答此题的关键是明白:这个最大正方形的对角线应等于圆的直径,据此即可画出符合要求的正方形.
图二:②3.14×22﹣2×2×2×2÷2,
=12.56﹣8,
=4.56(平方厘米),
答:圆的面积比正方形的面积大4.56平方厘米.
故答案为:4.56.

练习册系列答案
相关题目