题目内容
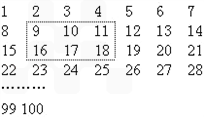
 将自然数排列如图,在这个数阵里,小明用正方形框出九个数.
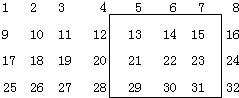
将自然数排列如图,在这个数阵里,小明用正方形框出九个数.(1)任意移动几次,每次框住的9个数和与中间的数有什么关系?
(2)如果框住的9个数的和是225,你能求出中间的一个数吗?
(3)一共可以盖住多少个不同的和?
分析:(1)任意移动几次,仔细观察框中的9个数,先算出每次框住的9个数和,再找与中间数的关系即可;
(2)根据框住的9个数和是中间的数的9倍,解答即可;
(3)原来正方形框左右平移一共有6个,原来的正方形框上下平移一共有2个,一共就有6×2=12(个);
(2)根据框住的9个数和是中间的数的9倍,解答即可;
(3)原来正方形框左右平移一共有6个,原来的正方形框上下平移一共有2个,一共就有6×2=12(个);
解答:解:(1)(13+14+15+21+22+23+29+30+31)÷22,
=198÷22,
=9,
如果框出的9个数是1、2、3,9、10、11,17、18、19:
(1+2+3+9+10+11+17+18+19)÷10
=90÷10
=9,
所以发现每次框住的9个数和是中间的数的9倍;
答:每次框住的9个数和是中间的数的9倍;
(2)225÷9=25,
答:中间的一个数是25;
(3)6×2=12(个),
答:一共可以盖住12个不同的和.
故答案为:每次框住的9个数和是中间的数的9倍;25;12.
=198÷22,
=9,
如果框出的9个数是1、2、3,9、10、11,17、18、19:
(1+2+3+9+10+11+17+18+19)÷10
=90÷10
=9,
所以发现每次框住的9个数和是中间的数的9倍;
答:每次框住的9个数和是中间的数的9倍;
(2)225÷9=25,
答:中间的一个数是25;
(3)6×2=12(个),
答:一共可以盖住12个不同的和.
故答案为:每次框住的9个数和是中间的数的9倍;25;12.
点评:解答此题的关键是,根据所给的框法,及表中数的特点,即可找出它们之间的规律,再根据规律作答即可.

练习册系列答案
相关题目
 将自然数按如图顺序排列:
将自然数按如图顺序排列: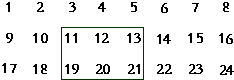 将自然数排列如图,在这个数阵里,John用长方形框出二行六个数(图中长方形框仅为示意),如果框出来的六个数的和是432,你知道John框出的这六个数中最小的那个数是多少吗?
将自然数排列如图,在这个数阵里,John用长方形框出二行六个数(图中长方形框仅为示意),如果框出来的六个数的和是432,你知道John框出的这六个数中最小的那个数是多少吗? (2012?郑州模拟)将自然数1~100排列如图:
(2012?郑州模拟)将自然数1~100排列如图: