题目内容
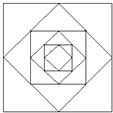如图中有六个正方形，较小的正方形都由较大的正方形的四边中点连接而成．已知最大的正方形的边长为16厘米，那么最小的正方形的面积等于分析：我们先分析最外两层：
，在图中添两条辅助线（虚线），不难看出三角形1、2、3、4、5、6、7、8的面积是相等的．进而推断，由三角形2、4、6、8组成的较小正方形的面积是大正方形面积的一半，即：256÷2=128平方厘米．以此类推，每个较小正方形面积都是与之最近的较大正方形面积的一半，于是，用128÷2÷2÷2÷2=8平方厘米，便求出了题中最小的正方形的面积是8平方厘米．
，在图中添两条辅助线（虚线），不难看出三角形1、2、3、4、5、6、7、8的面积是相等的．进而推断，由三角形2、4、6、8组成的较小正方形的面积是大正方形面积的一半，即：256÷2=128平方厘米．以此类推，每个较小正方形面积都是与之最近的较大正方形面积的一半，于是，用128÷2÷2÷2÷2=8平方厘米，便求出了题中最小的正方形的面积是8平方厘米．解答：解：16×16÷2÷2÷2÷2÷2
=256÷2÷2÷2÷2÷2
=8（平方厘米）．
答：最小的正方形的面积等于 8平方厘米．
故答案为：8．
=256÷2÷2÷2÷2÷2
=8（平方厘米）．
答：最小的正方形的面积等于 8平方厘米．
故答案为：8．
点评：考查了数与形结合的规律，图中的六个正方形，由外到内，依次为外面正方形的一半，依此即可求解．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
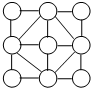在如图中，有六个不同的正方形，把1-9九个自然数填入九个○内，使每个正方形的四个顶点上的和相等．
如图中有六个正方形，较小的正方形都由较大的正方形的四边中点连接而成．已知最大的正方形的边长为10厘米，那么最小的正方形的面积等于
10、一个棱长为1的小正方体形状的骰子，它的六个面上各写有一个大写英文字母D、E、G、I、N、O中的一个．先将它放在由20个边长为1的小正方形拼成的4×5的棋盘的左上角的小方格上，令字母D朝上（如图所示），然后将它连续的向邻格翻动，并且恰好经过4×5棋盘上的其余的19个小方格各1次（共翻动了19次），最终停止在棋盘的右下角的小方格上．如果图中小方格中给定的字母是骰子在翻动到该小方格上时，骰子朝上的面上所写的字母（字母可“正放”、“横放”或“倒放”）．那么，骰子翻动到画有“﹡”的小方格时，骰子朝上的面所写的字母是（ ）