题目内容
【题目】有大、小两个盒子,其中大盒内装1001枚白棋和1000枚同样大小的黑棋子,小盒内装有足够多的黑棋.康康每次从大盒内随意摸出两枚棋子:若摸出的两枚棋子同色,则从小盒内取一枚黑子放入大盒内;若摸出的两枚棋子异色,则把其中白棋子放回大盒内.问:从大盒内摸了1999次棋子后,大盒内还剩几枚棋子?它们都是什么颜色?
【答案】2,1黑1白
【解析】首先分析在操作条件下会出现的各种可能情况:
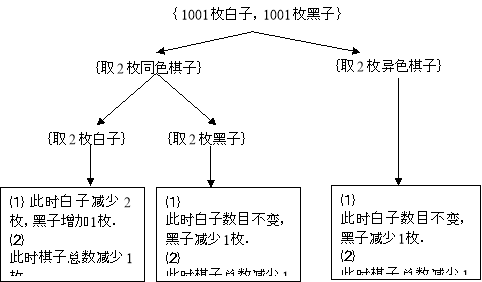
通过上面分析可知,每操作一次棋子的总数都要减少1枚,所以在不断操作下去的过程中,总棋子数将越来越少.摸了1999次棋子后,大盒内的棋子要减少1999枚,此时大盒内还剩:![]() (枚),
(枚),
接下来要分析这2枚棋子会是什么颜色呢?
注意到每操作一次黑子数不是增加一枚就是减少一枚,而相邻两个自然数的奇偶性不同.所以,开始时有1000枚黑子,是一个偶数,那么,第一次操作后黑子数目将变为奇数,接下来黑子数目又将变为偶数![]() 这样一来,黑子数目的奇偶性将呈现下列规律:
这样一来,黑子数目的奇偶性将呈现下列规律:

显然,根据上述规律,第1999次操作后黑子数将有奇数枚.而此时大盒中仅剩2枚棋子,所以必然是1枚白子1枚黑子.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小小统计员.
王林家2013年下半年用水情况统计图
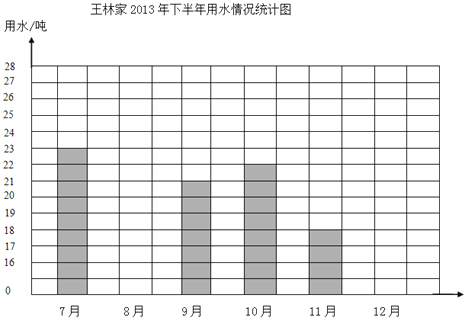
王林家2013年下半年用水情况统计表
月份 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
用水/吨 | 26 | 21 | 18 | 16 |
(1)把统计图和统计表补充完整.
(2) 月份用水最多, 月份用水最少.
(3)下半年王林家平均每月用水多少吨?
(4)你还能提出什么数学问题?(提2个)