题目内容
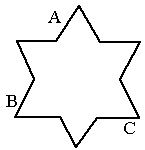
如图,在等边三角形ABC中,AD=3DB,DE⊥BC.如果三角形BED的面积是1平方厘米,则三角形ABC的面积是
32
32
平方厘米.
分析:
如图,从点A向底边BC作垂线AF交BC于点F,由题意知△ABC是等边三角形,则三线合一,BC=2BF,由AD=3DB,得AB=4BD,由DE⊥BC,AF⊥BC,可得BF=4BE,AF=4DE,找出BC与
BE的关系,AF与DE的关系,根据△面积公式可推出.

如图,从点A向底边BC作垂线AF交BC于点F,由题意知△ABC是等边三角形,则三线合一,BC=2BF,由AD=3DB,得AB=4BD,由DE⊥BC,AF⊥BC,可得BF=4BE,AF=4DE,找出BC与
BE的关系,AF与DE的关系,根据△面积公式可推出.
解答:解:因为△ABC是等边三角形,
又因为DE⊥BC,AF⊥BC,AD=3DB,
所以点E也是BF的4分点,,点F是BC的中点,
所以BF=4BE,AF=4DE,
所以S△ABF=16S△BED,
因为S△ABC=2S△ABF,
所以S△ABC=2×16S△BED,
=32S△BED,
因为三角形BED的面积是1平方厘米,
所以S△ABC=1×32(平方厘米).
答:三角形ABC的面积是32平方厘米.
故答案为:32.
又因为DE⊥BC,AF⊥BC,AD=3DB,
所以点E也是BF的4分点,,点F是BC的中点,
所以BF=4BE,AF=4DE,
所以S△ABF=16S△BED,
因为S△ABC=2S△ABF,
所以S△ABC=2×16S△BED,
=32S△BED,
因为三角形BED的面积是1平方厘米,
所以S△ABC=1×32(平方厘米).
答:三角形ABC的面积是32平方厘米.
故答案为:32.
点评:此题重点要知道等边三角形三线合一的特性,找出△BED的边和高与△ABC的边和高之间的关系.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
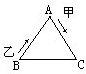 如图,等边三角形ABC的边长为100米,甲自A点,乙自B点同时出发,按顺时针方向沿着三角形的边行进.甲每分钟走60米,乙每分钟走90米,在过每个顶点时各人都因转弯而耽误10秒钟,那么乙在出发
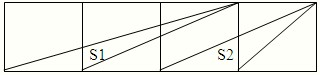
如图,等边三角形ABC的边长为100米,甲自A点,乙自B点同时出发,按顺时针方向沿着三角形的边行进.甲每分钟走60米,乙每分钟走90米,在过每个顶点时各人都因转弯而耽误10秒钟,那么乙在出发 如图,在等边三角形ABC上有两个动点D、E,动点D从A出发到B,每秒移动1厘米,动点E以每秒4厘米的速度在AC间往返运动.D、E两点同时从A点出发,随时连结DE两点,在D由A到B的这段时间内,线段DE与三角形的一部分构成的最小梯形面积是18平方厘米(图中阴影部分).三角形ABC的面积是多少平方厘米?
如图,在等边三角形ABC上有两个动点D、E,动点D从A出发到B,每秒移动1厘米,动点E以每秒4厘米的速度在AC间往返运动.D、E两点同时从A点出发,随时连结DE两点,在D由A到B的这段时间内,线段DE与三角形的一部分构成的最小梯形面积是18平方厘米(图中阴影部分).三角形ABC的面积是多少平方厘米?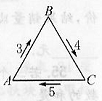 一只蚂蚁沿边长为240cm的等边三角形ABC的三条边由A点顺时针爬行一周.它在三条边上的速度分别是每秒3cm,4cm,5cm(如图).且当它到达拐点(A,B,C)时会休息26秒,当它爬完一周回到点A时,行程结束.这期间,蚂蚁的平均速度是
一只蚂蚁沿边长为240cm的等边三角形ABC的三条边由A点顺时针爬行一周.它在三条边上的速度分别是每秒3cm,4cm,5cm(如图).且当它到达拐点(A,B,C)时会休息26秒,当它爬完一周回到点A时,行程结束.这期间,蚂蚁的平均速度是