题目内容
 在如图的用七巧板拼成的正方形中,所有三角形面积的和,是大正方形面积的________倍.
在如图的用七巧板拼成的正方形中,所有三角形面积的和,是大正方形面积的________倍.
1
分析:如图,根据七巧板的特点可得:设大正方形的边长是1,则可得三角形ABC的面积是1×1÷2= ;则三角形ABH和三角形BCH的面积就是
;则三角形ABH和三角形BCH的面积就是 ×
× =
= ;三角形DEF的面积等于
;三角形DEF的面积等于 ×
× ×
× =
= ;三角形KMH的面积=三角形FGC的面积=
;三角形KMH的面积=三角形FGC的面积= ×
× =
= ;据此把它们加起来即可得出所以的三角形的面积之和,再除以大正方形的面积即可解答.
;据此把它们加起来即可得出所以的三角形的面积之和,再除以大正方形的面积即可解答.
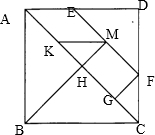
解答:设大正方形的边长是1,
则可得三角形ABC的面积是1×1÷2= ;
;
所以三角形ABH和三角形BCH的面积就是 ×
× =
= ;
;
三角形DEF的面积等于 ×
× ×
× =
= ;
;
三角形KMH的面积=三角形FGC的面积= ×
× =
= ;
;
所以三角形的面积之和是: +
+ ×2+
×2+ +
+ ×2=1
×2=1 ,
,
大正方形的面积是1×1=1,
所以1 ÷1=1
÷1=1 ,
,
答:所有的三角形的面积之和是大正方形的面积的1 倍.
倍.
故答案为:1 .
.
点评:解答本题要充分利用正方形的特殊性质,设大正方形的边长是1,从而得出各个小三角形的边长,再利用三角形的面积公式计算即可解答.

分析:如图,根据七巧板的特点可得:设大正方形的边长是1,则可得三角形ABC的面积是1×1÷2=
 ;则三角形ABH和三角形BCH的面积就是
;则三角形ABH和三角形BCH的面积就是 ×
× =
= ;三角形DEF的面积等于
;三角形DEF的面积等于 ×
× ×
× =
= ;三角形KMH的面积=三角形FGC的面积=
;三角形KMH的面积=三角形FGC的面积= ×
× =
= ;据此把它们加起来即可得出所以的三角形的面积之和,再除以大正方形的面积即可解答.
;据此把它们加起来即可得出所以的三角形的面积之和,再除以大正方形的面积即可解答.
解答:设大正方形的边长是1,
则可得三角形ABC的面积是1×1÷2=
 ;
;所以三角形ABH和三角形BCH的面积就是
 ×
× =
= ;
;三角形DEF的面积等于
 ×
× ×
× =
= ;
;三角形KMH的面积=三角形FGC的面积=
 ×
× =
= ;
;所以三角形的面积之和是:
 +
+ ×2+
×2+ +
+ ×2=1
×2=1 ,
,大正方形的面积是1×1=1,
所以1
 ÷1=1
÷1=1 ,
,答:所有的三角形的面积之和是大正方形的面积的1
 倍.
倍.故答案为:1
 .
.点评:解答本题要充分利用正方形的特殊性质,设大正方形的边长是1,从而得出各个小三角形的边长,再利用三角形的面积公式计算即可解答.

练习册系列答案
相关题目
 在如图的用七巧板拼成的正方形中,所有三角形面积的和,是大正方形面积的
在如图的用七巧板拼成的正方形中,所有三角形面积的和,是大正方形面积的 用一块边长为6cm的正方形ABCD厚纸板做一套七巧板(如图1),现用它拼成一只“小猫”的图案(如图2)请你根据图案及“猫头”上的字母回答下列问题:
用一块边长为6cm的正方形ABCD厚纸板做一套七巧板(如图1),现用它拼成一只“小猫”的图案(如图2)请你根据图案及“猫头”上的字母回答下列问题: