题目内容
【题目】如图,把正三角形的每边三等分,将各边的中间段取来向外作小正三角形,得到一个六角形,再将这个六角形的六个“角”(即小正三角形)的两边三等分,又以它的中间段向外作更小的正三角形,这样就得到了如图所示的图形.如果作出的每个小三角形的面积是1,那么原图形的面积是 . 
【答案】81
【解析】解:每个小三角形的边长都是相等的,那么IG:AD=1:3,
又因为三角形GHI和三角形AFD是相似三角形,所以S△GHI:S△AFD=1:32=1:9;
同理,AD:AC=1:3,又因为三角形ABC和三角形AFD是相似三角形,所以S△AFD:S△ABC=1:32=1:9;
那么S△GHI:S△ABC=1:(9×9)=1:81,
又因为,S△GHI=1,
所以,原图形的面积是S△ABC=1×81=81.
故答案为:81.
根据题意可得:每个小三角形的边长都是相等的,那么IG:AD=1:3,又因为三角形GHI和三角形AFD是相似三角形,所以S△GHI:S△AFD=1:32=1:9;同理,AD:AC=1:3,又因为三角形ABC和三角形AFD是相似三角形,所以S△AFD:S△ABC=1:32=1:9;那么S△GHI:S△ABC=1:(9×9)=1:81,再根据每个小三角形的面积是1,即可求出原图形的面积.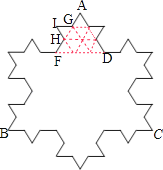

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】用自己喜欢的方法计算.
5.6×0.7+0.2×5.6+0.56 | 0.9+99×0.9 | 89×[34﹣(716﹣14)] |
720﹣800÷16 | [12﹣(34﹣35 )]÷710 | 8.5÷[(1+0.5)×5] |

