题目内容
操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.探究:设A、P两点间的距离为x
(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到的结论;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式,并写出函数的自变量取值范围;
(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由.
(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到的结论;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式,并写出函数的自变量取值范围;
(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由.
分析:(1)过点P作PE⊥BC于E,作PF⊥CD于F,根据正方形的对角线平分一组对角可得AC平分∠BCD,根据角平分线上的点到角的两边的距离相等可得PE=PF,然后求出∠EPF=90°,根据同角的余角相等求出∠1=∠2,然后利用“角边角”证明△BPE和△QPF全等,根据全等三角形对应边相等即可得证;
(2)先求出四边形PECF是正方形,再根据全等三角形的面积相等得到四边形PBCQ的面积等于正方形PECF的面积,然后根据正方形的性质表示出PC,再根据正方形的面积等于对角线平方的一半列式整理即可得解;
(3)延长BP交CD于G,根据点Q在DC的延长线上判断出∠PCQ>90°,从而得到PC=QC,根据等边对等角可得∠1=∠2,然后根据同角的余角相等求出∠3=∠5,再根据两直线平行,内错角相等可得∠4=∠5,根据等角对等边的想可得AB=AP,从而得解.
(2)先求出四边形PECF是正方形,再根据全等三角形的面积相等得到四边形PBCQ的面积等于正方形PECF的面积,然后根据正方形的性质表示出PC,再根据正方形的面积等于对角线平方的一半列式整理即可得解;
(3)延长BP交CD于G,根据点Q在DC的延长线上判断出∠PCQ>90°,从而得到PC=QC,根据等边对等角可得∠1=∠2,然后根据同角的余角相等求出∠3=∠5,再根据两直线平行,内错角相等可得∠4=∠5,根据等角对等边的想可得AB=AP,从而得解.
解答:解:(1)结论:PQ=PB.
证明:如图1,过点P作PE⊥BC于E,作PF⊥CD于F,
∵正方形ABCD,
∴∠BCD=90°,AC平分∠BCD,
又∵PE⊥BC于E,PF⊥DC于F,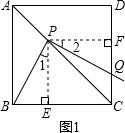
∴PE=PF,
∵PE⊥BC,PF⊥DC,∠BCD=90°,
∴∠EPF=90°,
∴∠2+∠EPQ=90°,
又∵∠1+∠EPQ=∠BPQ=90°,
∴∠1=∠2,
∵在△BPE和△QPF中
∴△BPE≌△QPF(ASA),
∴PB=PQ;
(2)解:∵∠PEC=∠PFC=∠ECF=90°,
∴四边形PECF是矩形,
又∵PE=PF,
∴四边形PECF是正方形,
∵正方形ABCD,AB=1,
∴AC=
,
∵AP=x,
∴PC=
-x,
由(1)知△BPE≌△QPF,
∴S△BPE=S△QPF,
∴S四边形PBCQ=S正方形PECF,
∴S四边形PBCQ=
PC2=
(
-x)2=
x2-
x+1,
即y=
x2-
x+1,
∵点Q在CD上,
∴PC>PQ,
∴
-x>
,
解得x<
,
所以,x的取值范围是0≤x<
;
(3)解:如图2,延长BP交DC于G,
∵点Q在DC的延长线上,
∴∠PCQ>90°,
∴∴等腰△PCQ中,PC=QC,
∴∠1=∠2,
∵∠BPQ=90°,
∴∠1+∠5=90°,∠2+∠3=90°,
∵∠1=∠2,
∴∠5=∠3,
在正方形ABCD中,AB∥DC,
∴∠4=∠5,
∴∠4=∠3,
∴AP=AB,
∴x=1.
证明:如图1,过点P作PE⊥BC于E,作PF⊥CD于F,
∵正方形ABCD,
∴∠BCD=90°,AC平分∠BCD,
又∵PE⊥BC于E,PF⊥DC于F,

∴PE=PF,
∵PE⊥BC,PF⊥DC,∠BCD=90°,
∴∠EPF=90°,
∴∠2+∠EPQ=90°,
又∵∠1+∠EPQ=∠BPQ=90°,
∴∠1=∠2,
∵在△BPE和△QPF中
|
∴△BPE≌△QPF(ASA),
∴PB=PQ;
(2)解:∵∠PEC=∠PFC=∠ECF=90°,
∴四边形PECF是矩形,
又∵PE=PF,
∴四边形PECF是正方形,
∵正方形ABCD,AB=1,
∴AC=
| 2 |
∵AP=x,
∴PC=
| 2 |
由(1)知△BPE≌△QPF,
∴S△BPE=S△QPF,
∴S四边形PBCQ=S正方形PECF,
∴S四边形PBCQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
即y=
| 1 |
| 2 |
| 2 |
∵点Q在CD上,
∴PC>PQ,
∴
| 2 |
| ||
| 2 |

解得x<
| ||
| 2 |
所以,x的取值范围是0≤x<
| ||
| 2 |
(3)解:如图2,延长BP交DC于G,
∵点Q在DC的延长线上,
∴∠PCQ>90°,
∴∴等腰△PCQ中,PC=QC,
∴∠1=∠2,
∵∠BPQ=90°,
∴∠1+∠5=90°,∠2+∠3=90°,
∵∠1=∠2,
∴∠5=∠3,
在正方形ABCD中,AB∥DC,
∴∠4=∠5,
∴∠4=∠3,
∴AP=AB,
∴x=1.
点评:本题考查了正方形的性质,全等三角形的判定与性质,等腰三角形的性质,正方形的问题,往往通过作辅助线构造出全等三角形求解.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
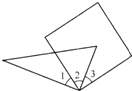 如图,将一把三角尺与一个正方形叠放在一起,其中相等的角是
如图,将一把三角尺与一个正方形叠放在一起,其中相等的角是 对多边形定义一种“延展”操作:将其每一边AB变成向外凸的折线ACDEB,其中C和E是AB的三等分点,CDE构成等边三角形,如图,则一个边长是1的等边三角形,经两次“延展”操作得到的图形的周长是
对多边形定义一种“延展”操作:将其每一边AB变成向外凸的折线ACDEB,其中C和E是AB的三等分点,CDE构成等边三角形,如图,则一个边长是1的等边三角形,经两次“延展”操作得到的图形的周长是