题目内容
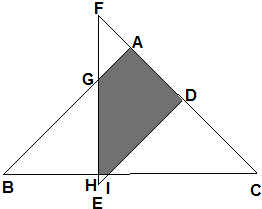
两个等腰直角三角形重叠如图,求图中阴影部分面积.(单位:厘米)


分析:为了便于分析,标上各字母,如下图所示:

由等腰直角三角形的性质,可知图中所有的三角形都为等腰直角三角形.因此CI=CF=1厘米,DE=EF=3厘米,BC=AF=4厘米,于是由线段的和差可以求出线段EC,BE的长度,由GE=BE,可得GE的长度,于是用DE-GE,可求得DG的长度,再由三角形DGH是等腰直角三角形,斜边上的高是斜边的一半,可知DG边上的高等于DG的一半,于是利用三角形的面积公式就可以求出三角形DGH的面积,再由梯形的面积公式求得梯形DECI的面积,相减即可求得阴影部分的面积.

由等腰直角三角形的性质,可知图中所有的三角形都为等腰直角三角形.因此CI=CF=1厘米,DE=EF=3厘米,BC=AF=4厘米,于是由线段的和差可以求出线段EC,BE的长度,由GE=BE,可得GE的长度,于是用DE-GE,可求得DG的长度,再由三角形DGH是等腰直角三角形,斜边上的高是斜边的一半,可知DG边上的高等于DG的一半,于是利用三角形的面积公式就可以求出三角形DGH的面积,再由梯形的面积公式求得梯形DECI的面积,相减即可求得阴影部分的面积.
解答:解:由等腰直角三角形的性质可得,CI=CF=1厘米,DE=EF=3厘米,BC=AF=4厘米,
所以EC=EF-CF=3-1=2(厘米),
BE=BC-EC=4-2=2(厘米),
所以GE=BE=2厘米,
DG=DE-GE=3-2=1(厘米),
由等腰直角三角形的性质可知三角形DGH的斜边DG上的高为:1÷2=
(厘米),
所以三角形DGH的面积是:1×
÷2=
(平方厘米),
梯形DECI的面积是:(1+3)×2÷2=4(平方厘米),
所以阴影部分的面积是:4-
=3.75(平方厘米).
答:阴影部分的面积是3.75平方厘米.
所以EC=EF-CF=3-1=2(厘米),
BE=BC-EC=4-2=2(厘米),
所以GE=BE=2厘米,
DG=DE-GE=3-2=1(厘米),
由等腰直角三角形的性质可知三角形DGH的斜边DG上的高为:1÷2=
| 1 |
| 2 |
所以三角形DGH的面积是:1×
| 1 |
| 2 |
| 1 |
| 4 |
梯形DECI的面积是:(1+3)×2÷2=4(平方厘米),
所以阴影部分的面积是:4-
| 1 |
| 4 |
答:阴影部分的面积是3.75平方厘米.
点评:本题考查组合图形的面积,关键是求出三角形DGH的面积,另外,对等腰三角形性质的认识非常重要.

练习册系列答案
相关题目
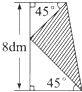 如图,一块梯形铁皮被剪走了一个直角三角形,刚好剩下两个等腰直角三角形,如果剪走部分的面积是梯形的一半,剪走部分面积是多少?
如图,一块梯形铁皮被剪走了一个直角三角形,刚好剩下两个等腰直角三角形,如果剪走部分的面积是梯形的一半,剪走部分面积是多少?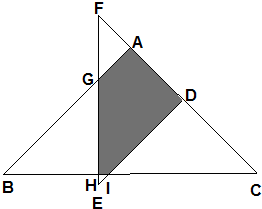
 在大小相等的两个等腰直角三角形中,各内接一个正方形(如图a,图b所示).如果图a中的内接正方形的面积是441平方厘米,那么图b中的内接正方形的面积是多少平方厘米?
在大小相等的两个等腰直角三角形中,各内接一个正方形(如图a,图b所示).如果图a中的内接正方形的面积是441平方厘米,那么图b中的内接正方形的面积是多少平方厘米?