题目内容
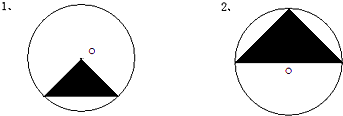
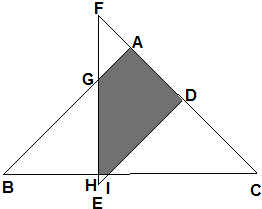
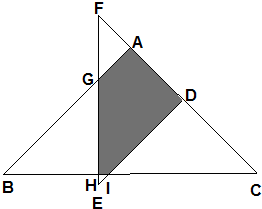
如图,两个等腰直角三角形叠放在一起,AF长3,AC长12,DE长8,重叠部份(阴影部份)五边形AGHID的面积是
22.25
22.25
.
分析:在直角梯形AGED中,分别求出AG=AF=3,DE=DF=8,DA=DF-AF=8-3=5,根据面积公式求得直角梯形AGED的面积,再求出直角等腰三角形IHE的面积,由直角梯形AGED的面积-直角等腰三角形IHE的面积即可求解.
解答:解:AF=AG=3,DE=DF=8,
所以:DA=DF-AF=8-3=5,
所以,直角梯形AGED的面积为:(3+8)×5÷2=27.5;
DC=AC-AD=12-5=7,DI=DC=7,
所以:IE=DE-DI=8-7=1,
直角等腰三角形IHE的面积为1×1÷4=0.25
所以,图中阴影部分的面积为:27.5-0.25=27.25.
故答案为:27.25.
所以:DA=DF-AF=8-3=5,
所以,直角梯形AGED的面积为:(3+8)×5÷2=27.5;
DC=AC-AD=12-5=7,DI=DC=7,
所以:IE=DE-DI=8-7=1,
直角等腰三角形IHE的面积为1×1÷4=0.25
所以,图中阴影部分的面积为:27.5-0.25=27.25.
故答案为:27.25.
点评:考查了组合图形的面积,本题可以将阴影部分的面积由直角梯形AGED的面积-直角等腰三角形IHE的面积得出,有一定的难度,关键是熟悉等腰直角三角形的性质.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
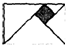 如图,四个等腰直角三角形和一个正方形拼成了一个长方形,已知正方形的面积为4平方厘米,则长方形的面积是
如图,四个等腰直角三角形和一个正方形拼成了一个长方形,已知正方形的面积为4平方厘米,则长方形的面积是 如图,5个等腰直角三角形叠放在一起,它们的斜边都在一条直线上,已知最小的等腰直角三角形的斜边长是4厘米,其余等腰三角形的斜边依次多4厘米,则图中阴影部分的面积
如图,5个等腰直角三角形叠放在一起,它们的斜边都在一条直线上,已知最小的等腰直角三角形的斜边长是4厘米,其余等腰三角形的斜边依次多4厘米,则图中阴影部分的面积