题目内容

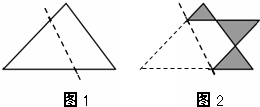图1是一个三角形，沿虚线折叠后得到图2，这个多边形的面积是原三角形面积的
79
，已知图2中阴影部分的面积和为15平方厘米，那么原三角形的面积是
27
27
平方厘米．
分析：先设原三角形面积为x平方厘米，再由阴影部分的面积为15平方厘米，可得图2的面积为：
x+15
2
=
x-15
2
-15，求出x的值即可．
解答：解：设原三角形面积为x平方厘米，
图2的面积为：
  
x+15
2
=
x-15
2
-15，
由题意得：
x+15
2
：x=
7
9
，
9（x+15）=2×7x，
   9x+135=14x，
       5x=135，
        x=27．
答：原三角形的面积是27平方厘米．
故答案为：27．
点评：本题考查的是三角形的面积及等积变换，根据题意求出图2的面积是解答此题的关键．
练习册系列答案
相关题目
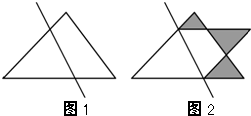图1是一个三角形，沿虚线折叠后得到图2，这个多边形的面积是原三角形面积的
7
9
．已知图2中阴影部分的面积和为15平方厘米，那么原三角形的面积是（　　）平方厘米．
阅读下列材料，并解决后面的问题．
★阅读材料：
我国是历史上较早发现并运用“勾股定理”的国家之一．我中古代把直角三角形中较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”，“勾股定理”因此而得名．
勾股定理：如果直角三角形两直角边长分别为a，b，斜边长为c，那么a2+b2=c2．即直角三角形两直角边的平方和等于斜边的平方．请运用“勾股定理”解决以下问题：

（1）如图一，分别以直角三角形的边为边长作正方形，其中s1=400，s2=225，则s3=
625
625
．
（2）如图二，是一个园柱形饮料罐，底面半径=8，高=15，顶面正中有一个小园孔，则一条直达底部的直吸管的最大长度是
17
17
．注：罐壁厚度和顶部园孔直径忽略不计．
（3）如图三，所示的直角三角形中，AB=6．则s1+s2的值=
13.5
13.5
． 注π值取3．
（4）如图四的圆柱，高=5厘米，底面半径=4厘米，在园柱底面A点有一只蚂蚁，它想吃到与A点相对的B点处的食物，需要爬行的路程是多少？小聪是这样思考的：
①将该园柱的侧面展开后得到一个长方形，如图五所示（A点的位置已经给出），请在图中中标出B点的位置并连接AB．
②小聪认为线段AB的长度是蚂蚁爬行的最短路程，那么蚂蚁爬行的最短路程是
13
13
厘米．注：π值取3．
（5）如图六，在长方形的底面A点有一只蚂蚁，想吃到上底面与A点相对的B点处的食物，它沿长方形表面爬行的最短路程是
15
15
厘米．

图1是一个三角形，沿虚线折叠后得到图2，这个多边形的面积是原三角形面积的数学公式．已知图2中阴影部分的面积和为15平方厘米，那么原三角形的面积是_____平方厘米．


  1. A.
    26
  2. B.
    27
  3. C.
    28
  4. D.
    29

阅读下列材料，并解决后面的问题．
★阅读材料：
我国是历史上较早发现并运用“勾股定理”的国家之一．我中古代把直角三角形中较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”，“勾股定理”因此而得名．
勾股定理：如果直角三角形两直角边长分别为a，b，斜边长为c，那么a2+b2=c2．即直角三角形两直角边的平方和等于斜边的平方．请运用“勾股定理”解决以下问题：

（1）如图一，分别以直角三角形的边为边长作正方形，其中s1=400，s2=225，则s3=________．
（2）如图二，是一个园柱形饮料罐，底面半径=8，高=15，顶面正中有一个小园孔，则一条直达底部的直吸管的最大长度是________．注：罐壁厚度和顶部园孔直径忽略不计．
（3）如图三，所示的直角三角形中，AB=6．则s1+s2的值=________． 注π值取3．
（4）如图四的圆柱，高=5厘米，底面半径=4厘米，在园柱底面A点有一只蚂蚁，它想吃到与A点相对的B点处的食物，需要爬行的路程是多少？小聪是这样思考的：
①将该园柱的侧面展开后得到一个长方形，如图五所示（A点的位置已经给出），请在图中中标出B点的位置并连接AB．
②小聪认为线段AB的长度是蚂蚁爬行的最短路程，那么蚂蚁爬行的最短路程是________厘米．注：π值取3．
（5）如图六，在长方形的底面A点有一只蚂蚁，想吃到上底面与A点相对的B点处的食物，它沿长方形表面爬行的最短路程是________厘米．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网