题目内容
把一个圆柱切拼成一个近似的长方体,这个长方体和原来的圆柱相比,( )
| A、体积、表面积都不变 | B、体积不变,表面积变大 | C、体积不变,表面积变小 |
分析:设圆柱的底面半径是r,然后表示出拼成的长方体的长与宽,长方体的高等于圆柱的高是h,再根据长方形的表面积和体积公式与圆柱的表面积和体积公式列式表示出长方体的表面积和体积与原来圆柱的表面积和体积,由此即可进行比较选择.
解答:解:设圆柱的底面半径是r,长方体的高等于圆柱的高是h,则长方形的长为πr,宽为r,
所以圆柱的表面积为:2πr2+2πrh;
圆柱的体积为:πr2h;
长方体的表面积为:(πr×r+πr×h+rh)×2=2πr2+2πrh+2rh;
长方体的体积为:πr×r×h=πr2h;
所以这个长方体和原来的圆柱体比较表面积变大了,体积没变.
故选:B.
所以圆柱的表面积为:2πr2+2πrh;
圆柱的体积为:πr2h;
长方体的表面积为:(πr×r+πr×h+rh)×2=2πr2+2πrh+2rh;
长方体的体积为:πr×r×h=πr2h;
所以这个长方体和原来的圆柱体比较表面积变大了,体积没变.
故选:B.
点评:本题是主要考查了圆柱的表面积和体积以及长方体的表面积和体积公式的灵活应用,根据圆柱切割拼组长方体的方法,正确表示出长方体的长宽高是解决本题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
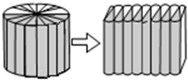 如图,把一个圆柱切拼成一个近似的长方体,这时长方体的表面积比原来增加了12平方厘米.如果截成两个小圆柱它的表面积增加了6.28平方厘米,求原来圆柱体的表面积
如图,把一个圆柱切拼成一个近似的长方体,这时长方体的表面积比原来增加了12平方厘米.如果截成两个小圆柱它的表面积增加了6.28平方厘米,求原来圆柱体的表面积