题目内容
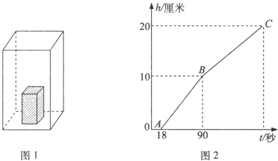 如图1,在底面积为100cm2、高为20cm的长方体水槽内放入一个长方体烧杯,以恒定不变的流量速度先向烧杯中注水,注满烧杯后,继续注水,直至注满水槽为止,此过程中,烧杯本身的质量、体积忽略不计,烧杯在大水槽中的位置始终不改变.水槽中水面上升的高度h(厘米)与注水时间t(秒)之间的关系如图2所示.
如图1,在底面积为100cm2、高为20cm的长方体水槽内放入一个长方体烧杯,以恒定不变的流量速度先向烧杯中注水,注满烧杯后,继续注水,直至注满水槽为止,此过程中,烧杯本身的质量、体积忽略不计,烧杯在大水槽中的位置始终不改变.水槽中水面上升的高度h(厘米)与注水时间t(秒)之间的关系如图2所示.(1)图2中点
A
A
表示烧杯中刚好注满水,点B
B
表示水槽中水面恰与烧杯中水面平齐;(2分)(2)求烧杯的底面积;(4分)
(3)求注水的速度及注满水槽所用的时间.(8分)
分析:(1)根据图示2的折线趋势可知:点A表示烧杯中刚好注满水,点B表示水槽内的水面高度恰好与烧杯中水面平齐;
(2)设烧杯的底面积为Scm2、高为h1cm,注水速度每秒为vcm3,注满水槽所用时间为t0.如图可知:当注水18秒时,烧杯刚好注满;当注水90秒时,水槽内的水面高度恰好是h1cm,根据100h1=90×
Sh1,求出S即可.
(3)由图可知注满烧杯和水槽一半所用的时间比是18:90=1:5,烧杯的体积:100×10÷5=200(cm3),注水速度:200÷18=
(立方厘米/秒);注满水槽所用时间:100×20÷
-=180(秒).
(2)设烧杯的底面积为Scm2、高为h1cm,注水速度每秒为vcm3,注满水槽所用时间为t0.如图可知:当注水18秒时,烧杯刚好注满;当注水90秒时,水槽内的水面高度恰好是h1cm,根据100h1=90×
| 1 |
| 18 |
(3)由图可知注满烧杯和水槽一半所用的时间比是18:90=1:5,烧杯的体积:100×10÷5=200(cm3),注水速度:200÷18=
| 100 |
| 9 |
| 100 |
| 9 |
解答:解:(1)点A表示烧杯中刚好注满水,点B表示水槽内的水面高度恰好与烧杯中水面平齐;
(2)设烧杯的底面积为Scm2、高为h1cm,注水速度为每秒vcm3,注满水槽所用时间为t0秒,由图2知,当注水18s时,烧杯刚好注满;当注水90s时,水槽内的水面高度恰好是h1cm(即烧杯高度).于是,Sh1=18v,100h1=90v
则有100h1=90×
Sh1,即S=20.
所以,烧杯的底面积为20cm2;
答:烧杯的底面积是20平方厘米
(3)由图可知注满烧杯和水槽一半所用的时间比是18:90=1:5,烧杯的体积:100×10÷5=200(cm3),
注水速度:200÷18=
(立方厘米/秒);
注满水槽所用时间:100×20÷
=180(秒);
答:注水的速度是
立方厘米/秒,注满水槽所用的时间是180秒.
(2)设烧杯的底面积为Scm2、高为h1cm,注水速度为每秒vcm3,注满水槽所用时间为t0秒,由图2知,当注水18s时,烧杯刚好注满;当注水90s时,水槽内的水面高度恰好是h1cm(即烧杯高度).于是,Sh1=18v,100h1=90v
则有100h1=90×
| 1 |
| 18 |
所以,烧杯的底面积为20cm2;
答:烧杯的底面积是20平方厘米
(3)由图可知注满烧杯和水槽一半所用的时间比是18:90=1:5,烧杯的体积:100×10÷5=200(cm3),
注水速度:200÷18=
| 100 |
| 9 |
注满水槽所用时间:100×20÷
| 100 |
| 9 |
答:注水的速度是
| 100 |
| 9 |
点评:此题主要考查是如何从折线统计图中获取信息,并根据信息结合图形回答问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图1,在棱长为4的正方体木块正中心挖掉一个底面边长为2、高为4的长方体木块.将5个图1中所示的正方体木块如图2叠放(空心部分朝上),且上面的正方体的四个顶点分别在下面四方体上面的中心处.那么图2中的几何体朝上的面面积为
如图1,在棱长为4的正方体木块正中心挖掉一个底面边长为2、高为4的长方体木块.将5个图1中所示的正方体木块如图2叠放(空心部分朝上),且上面的正方体的四个顶点分别在下面四方体上面的中心处.那么图2中的几何体朝上的面面积为
 如图1,在底面积为100cm2、高为20cm的长方体水槽内放入一个长方体烧杯,以恒定不变的流量速度先向烧杯中注水,注满烧杯后,继续注水,直至注满水槽为止,此过程中,烧杯本身的质量、体积忽略不计,烧杯在大水槽中的位置始终不改变.水槽中水面上升的高度h(厘米)与注水时间t(秒)之间的关系如图2所示.
如图1,在底面积为100cm2、高为20cm的长方体水槽内放入一个长方体烧杯,以恒定不变的流量速度先向烧杯中注水,注满烧杯后,继续注水,直至注满水槽为止,此过程中,烧杯本身的质量、体积忽略不计,烧杯在大水槽中的位置始终不改变.水槽中水面上升的高度h(厘米)与注水时间t(秒)之间的关系如图2所示.