题目内容
神机妙算(能简算的要写出简算过程)
(1)1
+2
+3
+…+10
=
(2)(1
×
+
)÷(1-
)=
(3)3.5÷1
+6.5×[12×(1
-0.3)-15%
(4)已知:
=
=
=20092010,求
的值.
(5)
+
+
+…+
.
(1)1
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 110 |
(2)(1
| 5 |
| 7 |
| 7 |
| 12 |
6
| ||||
|
| 1 |
| 11 |
(3)3.5÷1
| 1 |
| 3 |
| 1 |
| 3 |
(4)已知:
| a |
| 2 |
| b |
| 3 |
| c |
| 4 |
| 3a+b-2c |
| c-b+a |
(5)
| 1 |
| 1+2 |
| 1 |
| 1+2+3 |
| 1 |
| 1+2+3+4 |
| 1 |
| 1+2+3+4+…+10 |
分析:(1)把每个分数的整数部分与分数部分分别相加,整数部分用求和公式求出结果,分数部分的每个分数都可以拆成两个分数相减的形式,然后通过加减相抵消的方法,求出结果;
(2)此题的关键在于繁分式的化简,然后按运算顺序计算即可;
(3)把小数和百分数化为分数,计算较简便;
(4)因为20092010数字较大,设20092010=k,分别求出a、b、c的值,然后代入
,计算即可;
(5)
(2)此题的关键在于繁分式的化简,然后按运算顺序计算即可;
(3)把小数和百分数化为分数,计算较简便;
(4)因为20092010数字较大,设20092010=k,分别求出a、b、c的值,然后代入
| 3a+b-2c |
| c-b+a |
(5)
解答:解:(1)1
+2
+3
+…+10
,
=(1+2+3+…+10)+(
+
+
+…+
),
=(1+10)×10÷2+(1-
+
-
+
-
+…+
-
),
=55+(1-
),
=55+
,
=55
;
(2)(1
×
+
)÷(1-
),
=(
×
+
)÷(1-
),
=(1+9)÷
,
=10×
,
=11;
(3)3.5÷1
+6.5×[12×(1
-0.3)-15%],
=
×
+
×[12×(1
-
)-
],
=
+
×[12×
-
],
=
+
×[
-
],
=
+
×
,
=
+
,
=82.25;
(4)设200820092010=k,则a=2k,b=3k,c=4k,
则
,
=
,
=
,
=
;
(5)
+
+
+…+
,
=
+
+
+…+
,
=2×(
+
+…+
),
=2×(
-
+
-
+…
-
),
=2×(
-
),
=2×
,
=
.
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 110 |
=(1+2+3+…+10)+(
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 110 |
=(1+10)×10÷2+(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 10 |
| 1 |
| 11 |
=55+(1-
| 1 |
| 11 |
=55+
| 10 |
| 11 |
=55
| 10 |
| 11 |
(2)(1
| 5 |
| 7 |
| 7 |
| 12 |
6
| ||||
|
| 1 |
| 11 |
=(
| 12 |
| 7 |
| 7 |
| 12 |
| ||
|
| 1 |
| 11 |
=(1+9)÷
| 10 |
| 11 |
=10×
| 11 |
| 10 |
=11;
(3)3.5÷1
| 1 |
| 3 |
| 1 |
| 3 |
=
| 7 |
| 2 |
| 3 |
| 4 |
| 13 |
| 2 |
| 1 |
| 3 |
| 3 |
| 10 |
| 3 |
| 20 |
=
| 21 |
| 8 |
| 13 |
| 2 |
| 31 |
| 30 |
| 3 |
| 20 |
=
| 21 |
| 8 |
| 13 |
| 2 |
| 62 |
| 5 |
| 3 |
| 20 |
=
| 21 |
| 8 |
| 13 |
| 2 |
| 49 |
| 4 |
=
| 21 |
| 8 |
| 637 |
| 8 |
=82.25;
(4)设200820092010=k,则a=2k,b=3k,c=4k,
则
| 3a+b-2c |
| c-b+a |
=
| 3×2k+3k-2×4k |
| 4k-3k+2k |
=
| k |
| 3k |
=
| 1 |
| 3 |
(5)
| 1 |
| 1+2 |
| 1 |
| 1+2+3 |
| 1 |
| 1+2+3+4 |
| 1 |
| 1+2+3+4+…+10 |
=
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 10 |
| 1 |
| 55 |
=2×(
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 10×11 |
=2×(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 10 |
| 1 |
| 11 |
=2×(
| 1 |
| 2 |
| 1 |
| 11 |
=2×
| 9 |
| 22 |
=
| 9 |
| 11 |
点评:此题考查了分数的巧算,要根据数字特点,运用所学知识或运算技巧,灵活解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ×
×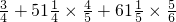 +71
+71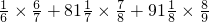
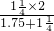 +2
+2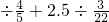
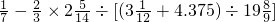
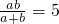 (a≠b),求
(a≠b),求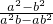 的值.
的值.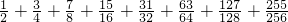 .
.