Question

9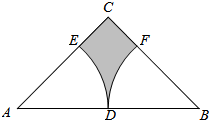．如图，在等腰直角三角形ABC中，∠C=90°，点D为AB的中点，已知扇形EAD和扇形FBD的圆心分别为点A、点B，且AC=2，则图中阴影部分的面积为2-$\frac{π}{2}$．

Answer 1

分析 用三角形ABC的面积减去扇形EAD和扇形FBD的面积，即可得出阴影部分的面积．

解答 解：因为BC=AC，∠C=90°，AC=2，
所以AB=2$\sqrt{2}$，
因为点D为AB的中点，
所以AD=BD=$\sqrt{2}$，
所以阴影部分的面积=三角形ABC的面积-扇形EAD的面积-扇形FBD的面积
=$\frac{1}{2}$×2×2-$\frac{45π（\sqrt{2}）^{2}}{360}$×2
=2-$\frac{π}{2}$
答：图中阴影部分的面积为2-$\frac{π}{2}$．
故答案为：2-$\frac{π}{2}$．

点评 本题考查了扇形面积的计算及等腰直角三角形的性质，熟记扇形的面积公式：S=$\frac{nπ{R}^{2}}{360}$是解答本题的关键．