题目内容
 如图,已知∠1+∠2=104°∠2+∠3=112°求∠1∠2∠3各是多少度.
如图,已知∠1+∠2=104°∠2+∠3=112°求∠1∠2∠3各是多少度.
解:由题意得:
∠1+∠2+∠2+∠3=(∠1+∠2+∠3)+∠2=104°+112°=216°,
∠2=216°-180°=36°;
∠1=104°-36°=68°;
∠3=112°-∠2=112°-36°=76°.
答:∠1是68度,∠2是36度,∠3是76度.
分析:因为三角形的三个内角和是180度,所以∠1+∠2+∠3=180°,由题意得:∠1+∠2+∠2+∠3=(∠1+∠2+∠3)+∠2=104°+112°=216°,所以∠2=216°-180°=36°,代入已知两个算式即可求出另外2个角的度数.
点评:解决本题要借助三角形的内角和是180度解答.
∠1+∠2+∠2+∠3=(∠1+∠2+∠3)+∠2=104°+112°=216°,
∠2=216°-180°=36°;
∠1=104°-36°=68°;
∠3=112°-∠2=112°-36°=76°.
答:∠1是68度,∠2是36度,∠3是76度.
分析:因为三角形的三个内角和是180度,所以∠1+∠2+∠3=180°,由题意得:∠1+∠2+∠2+∠3=(∠1+∠2+∠3)+∠2=104°+112°=216°,所以∠2=216°-180°=36°,代入已知两个算式即可求出另外2个角的度数.
点评:解决本题要借助三角形的内角和是180度解答.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
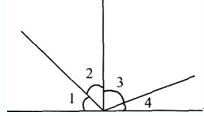
 如图,已知∠1+∠2=104°∠2+∠3=112°求∠1∠2∠3各是多少度.
如图,已知∠1+∠2=104°∠2+∠3=112°求∠1∠2∠3各是多少度.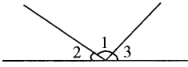
 如图,已知∠1=∠2=40°,∠3=
如图,已知∠1=∠2=40°,∠3=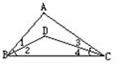 如图,已知∠1=∠2,∠3=∠4,∠A=80°.求∠BDC的度数.
如图,已知∠1=∠2,∠3=∠4,∠A=80°.求∠BDC的度数.