Question

4．两个人轮流往一个圆桌面上放同样大小的硬币，规则是：每人每次只能放一枚，硬币不许重叠，谁放完最后一枚硬币而使对方再无处可放，谁就获胜．那么先放着在（　　）处就必胜．

• A． 周长上
• B． 直径上
• C． 半径上
• D． 圆心上

Answer 1

分析 我们用对称的思想来分析一下．圆是关于圆心对称的图形，若A是圆内除圆心外的任意一点，则圆内一定有一点B与A关于圆心对称（其中AO=OB）如图：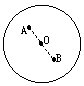

所以，圆内除圆心外，任意一点都有一个（关于圆心的）对称点．假设这两个人一个是甲，一个是乙，由此可以想到，只要甲把第一枚硬币放在圆桌面的圆心处，以后无论乙将硬币放在何处，甲一定能找到与之对称的点放置硬币．也就是说，只要乙能放，甲就一定能放．最后无处可放硬币的必是乙．

解答 解：假设这两个人一个是甲，一个是乙；甲的获胜策略是：
把第一枚硬币放到圆桌面的圆心处，以后总在乙上次放的硬币的对称点放置硬币．
答：如果甲先放，他要把第一枚硬币放到圆桌面的圆心处，以后总在乙上次放的硬币的对称点放置硬币，这样才能取胜．
故选：D．

点评 此题较难，应利用对称思想获胜，对称思想获胜策略体现出了一种机智，而这种机智来源于数学思想，应灵活运用数学知识解决问题．