题目内容
18.两根绳子,当第一根用去$\frac{2}{3}$,第二根用去$\frac{4}{5}$时,它们剩下的部分一样长.原来第一根与第二根绳长的比是3:5.分析 当第一根红用去$\frac{2}{3}$,可知剩下第一根绳长的(1-$\frac{2}{3}$);第二根用去$\frac{4}{5}$时,还剩下第二根绳长的(1-$\frac{4}{5}$);再根据“这时它们剩下的部分一样长”,可得出等量关系式:第一根的长度×(1-$\frac{2}{3}$)=第二根的长度×(1-$\frac{4}{5}$),然后把这个等式改写成比例即可解决问题.
解答 解:由分析可知:第一根的长度×(1-$\frac{2}{3}$)=第二根的长度×(1-$\frac{4}{5}$),
第一根的长度×$\frac{1}{3}$=第二根的长度×$\frac{1}{5}$,
即第一根的长度:第二根的长度=$\frac{1}{5}$:$\frac{1}{3}$=3:5;
故答案为:3,5.
点评 解决此题的关键是先求出第一根和第二根剩下的分率,进而结合题意,根据一个数乘分数的意义写出等式,再把等式改写成比例,化简即可.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
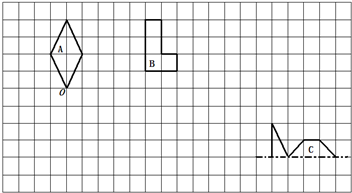 按要求画一画.
按要求画一画. 把如图所示的长方形铁皮卷成一个深20厘米的圆柱,配上一个底面做成一个圆柱形铁桶,铁桶的底面积是多少平方厘米?这个铁桶最多可以装水多少升?(铁皮的厚度忽略不计)
把如图所示的长方形铁皮卷成一个深20厘米的圆柱,配上一个底面做成一个圆柱形铁桶,铁桶的底面积是多少平方厘米?这个铁桶最多可以装水多少升?(铁皮的厚度忽略不计) 六年级同学血型情况如图:其中AB型血的同学是12人.
六年级同学血型情况如图:其中AB型血的同学是12人.