题目内容
14. 如图,纸上画了四个大小一样的圆,圆心分别是A、B、C、D,直线m通过A、B,直线n通过C、D,用S表示一个圆的面积,如果四个圆在纸上盖住的总面积是5(S-1),直线m、n之间被圆盖住的面积是8,阴影部分的面积是S1、S2、S3满足关系式S3=S2=S1,求S.
如图,纸上画了四个大小一样的圆,圆心分别是A、B、C、D,直线m通过A、B,直线n通过C、D,用S表示一个圆的面积,如果四个圆在纸上盖住的总面积是5(S-1),直线m、n之间被圆盖住的面积是8,阴影部分的面积是S1、S2、S3满足关系式S3=S2=S1,求S.
分析 观察图形可以得到四个圆之间的位置关系,根据重叠部分的面积可以列出一个方程,然后与题目中S1,S2,S3的关系联立方程组,解方程组得到S的值.
解答 解:由题设可得:$\left\{\begin{array}{l}{5(S-1)=4S-{S}_{1}-{S}_{2}-{S}_{3}}\\{{S}_{1}={S}_{2}={S}_{3}}\end{array}\right.$
所以S1=$\frac{5-S}{3}$ ①
又因为2S-$\frac{1}{2}$S1-S2-$\frac{1}{2}$S3=8,
即:2S-2S1=8 ②
把①代入②消去S1得:
2S-2×$\frac{5-S}{3}$=8
6S-10+2S=24
8S=34
S=$\frac{17}{4}$.
点评 本题考查的是圆与圆的位置关系,根据题意结合图形列方程组,用代入消元法解方程组求出S的值.

练习册系列答案
相关题目
2.表示一位病人一天内体温变化情况,绘制( )统计图比较合适.
| A. | 折线 | B. | 扇形 | C. | 条形 | D. | 以上都不对 |

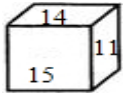 如图,立方体的六个面上标着连续的正整数,若相对的两个面上所标之数的和相等,则这六个数的和为81.
如图,立方体的六个面上标着连续的正整数,若相对的两个面上所标之数的和相等,则这六个数的和为81.