题目内容
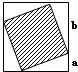 如图,4个相同的直角三角形围成了一个正方形,已知a:b=1:4,阴影部分占大正方形面积的
如图,4个相同的直角三角形围成了一个正方形,已知a:b=1:4,阴影部分占大正方形面积的68
68
%分析:根据题意可知,阴影部分的边长等于直角三角形的斜边的长,已知直角三角形两条直角边的比是1:4,大正方形的边长等于两条直角边的和,根据正方形的面积=边长×边长,先求出大正方形的面积,把大正方形的面积看作单位“1”,再求出四个直角三角形占大正方形的几分之几,再用单位“1”减去四个直角三角形占大正方形的几分之几,就求出了中间的正方形的面积占大正方形面积的几分之几,然后把分数化成百分数即可.
解答:解:大正方形的边长等于两条直角边的和,即1+4=5;
1-1×4÷2×4÷52,
=1-8÷25,
=1-
,
=
,
=68%;
答:阴影部分占大正方形面积的68%.
故答案为:68%.
1-1×4÷2×4÷52,
=1-8÷25,
=1-
| 8 |
| 25 |
=
| 17 |
| 25 |
=68%;
答:阴影部分占大正方形面积的68%.
故答案为:68%.
点评:此题主要考查正方形面积的计算,解答关键是求出大正方形的面积,把它看作 单位“1”,再求出4个三角形的面积正方形的面积占大正方形面积的几分之几,用单位“1”减4个三角形占大正方形的几分之几即可.由此解决问题.

练习册系列答案
相关题目
 学校计划建一个由8个完全相同的等腰直角三角形拼成的花坛(如图).已知每个三角形的直角边长4米,求这个花坛的面积.
学校计划建一个由8个完全相同的等腰直角三角形拼成的花坛(如图).已知每个三角形的直角边长4米,求这个花坛的面积.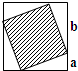 如图,4个相同的直角三角形围成了一个正方形,已知a:b=1:2,阴影部分的面积占大正方形面积的
如图,4个相同的直角三角形围成了一个正方形,已知a:b=1:2,阴影部分的面积占大正方形面积的 如图,4个相同的直角三角形围成了一个正方形,已知a:b=1:2,阴影部分的面积占大正方形面积的
如图,4个相同的直角三角形围成了一个正方形,已知a:b=1:2,阴影部分的面积占大正方形面积的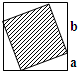 如图,4个相同的直角三角形围成了一个正方形,已知a:b=1:2,阴影部分的面积占大正方形面积的________.
如图,4个相同的直角三角形围成了一个正方形,已知a:b=1:2,阴影部分的面积占大正方形面积的________.