题目内容
如图所示,力F拉着小球使小球在光滑半圆柱表面缓缓上升过程中,小球受到的拉力和支持力的变化情况是(圆柱体的圆心在滑轮的正下方)( )
 |
试题答案
C| A.拉力不变,支持力变大 | B.拉力变小,支持力变大 |
| C.拉力变小,支持力不变 | D.拉力变大,支持力不变 |
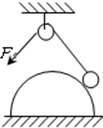

 如图所示,力F拉着小球使小球在光滑半圆柱表面缓缓上升过程中,小球受到的拉力和支持力的变化情况是(圆柱体的圆心在滑轮的正下方)
如图所示,力F拉着小球使小球在光滑半圆柱表面缓缓上升过程中,小球受到的拉力和支持力的变化情况是(圆柱体的圆心在滑轮的正下方)如图所示,力F拉着小球使小球在光滑半圆柱表面缓缓上升过程中,小球受到的拉力和支持力的变化情况是(圆柱体的圆心在滑轮的正下方):
A. 拉力不变,支持力变大 B. 拉力变小,支持力变大
C. 拉力变小,支持力不变 D. 拉力变大,支持力不变

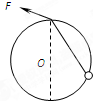 如图所示,固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔,质量为m的小球套在圆环上.一根细线的下端系着小球,上端穿过小孔用手拉住.现拉动细线,使小球沿圆环缓慢上移.在移动过程中手对线的拉力F和轨道对小球的弹力N的大小变化情况是( )
如图所示,固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔,质量为m的小球套在圆环上.一根细线的下端系着小球,上端穿过小孔用手拉住.现拉动细线,使小球沿圆环缓慢上移.在移动过程中手对线的拉力F和轨道对小球的弹力N的大小变化情况是( )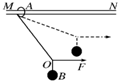 如图所示,轻绳的两端分别系在圆环A和小球B上,圆环A套在粗糙的水平直杆MN上.现用水平力F拉着绳子上的一点O,使小球B从图中实线位置缓慢上升到虚线位置,但圆环A始终保持在原位置不动.在这一过程中,环对杆的摩擦力Ff和环对杆的压力FN的变化情况是( )
如图所示,轻绳的两端分别系在圆环A和小球B上,圆环A套在粗糙的水平直杆MN上.现用水平力F拉着绳子上的一点O,使小球B从图中实线位置缓慢上升到虚线位置,但圆环A始终保持在原位置不动.在这一过程中,环对杆的摩擦力Ff和环对杆的压力FN的变化情况是( ) 如图所示,长为L的轻质细线,一端固定在O1,另一端固定一质量为m、电荷量为+q的小球,O1 O2为竖直线,其左侧存在着一个水平方向上的矩形形状的匀强电场,电场的下边界为水平线D O2,紧邻匀强电场的下边界停放着一个质量为M=2m的滑块,初始时刻M静止在光滑的水平面上,滑块M上是一个以O2为圆心光滑的四分之一圆弧,圆弧的最低点F与水平面相切与O2的正下方.在O1 O2竖直线的右侧的光滑水平面上停放着质量均为m、间距均为S的粘性小物块(即碰撞后立刻粘为一体).零时刻把小球拉到与O1 等高的A点使细线伸直,然后静止释放,小球摆到最左端的C点后返回,已知O1C与竖直方向的夹角θ=37°.小球和小物块都可以看成质点且都与滑块M处在同一竖直平面内如图所示.m、+q、L、θ为已知量,电场强度E、圆弧的半径R及BO2的高度h为未知量,空气阻力不计,重力加速度为g.
如图所示,长为L的轻质细线,一端固定在O1,另一端固定一质量为m、电荷量为+q的小球,O1 O2为竖直线,其左侧存在着一个水平方向上的矩形形状的匀强电场,电场的下边界为水平线D O2,紧邻匀强电场的下边界停放着一个质量为M=2m的滑块,初始时刻M静止在光滑的水平面上,滑块M上是一个以O2为圆心光滑的四分之一圆弧,圆弧的最低点F与水平面相切与O2的正下方.在O1 O2竖直线的右侧的光滑水平面上停放着质量均为m、间距均为S的粘性小物块(即碰撞后立刻粘为一体).零时刻把小球拉到与O1 等高的A点使细线伸直,然后静止释放,小球摆到最左端的C点后返回,已知O1C与竖直方向的夹角θ=37°.小球和小物块都可以看成质点且都与滑块M处在同一竖直平面内如图所示.m、+q、L、θ为已知量,电场强度E、圆弧的半径R及BO2的高度h为未知量,空气阻力不计,重力加速度为g.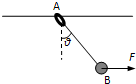 如图所示,质量均为m的环A与球B用一轻质细绳相连,环A套在水平喜感上.现有一水平恒力F作用在球B上,使A环与B球一起向右匀速运动.已知细绳与竖直方向的夹角为θ.下列说法中正确的是( )
如图所示,质量均为m的环A与球B用一轻质细绳相连,环A套在水平喜感上.现有一水平恒力F作用在球B上,使A环与B球一起向右匀速运动.已知细绳与竖直方向的夹角为θ.下列说法中正确的是( )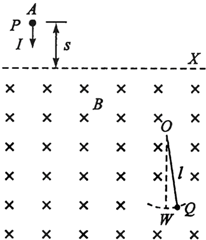 如图所示,水平虚线X下方区域分布着方向水平、垂直纸面向里、磁感应强度为B的匀强磁场,整个空间存在匀强电场(图中未画出).质量为m,电荷量为+q的小球P静止于虚线X上方A点,在某一瞬间受到方向竖直向下、大小为I的冲量作用而做匀速直线运动.在A点右下方的磁场中有定点O,长为l的绝缘轻绳一端固定于O点,另一端连接不带电的质量同为m的小球Q,自然下垂.保持轻绳伸直,向右拉起Q,直到绳与竖直方向有一小于50的夹角,在P开始运动的同时自由释放Q,Q到达O点正下方W点时速率为v0.P、Q两小球在W点发生正碰,碰后电场、磁场消失,两小球粘在一起运动.P、Q两小球均视为质点,P小球的电荷量保持不变,绳不可伸长,不计空气阻力,重力加速度为g.
如图所示,水平虚线X下方区域分布着方向水平、垂直纸面向里、磁感应强度为B的匀强磁场,整个空间存在匀强电场(图中未画出).质量为m,电荷量为+q的小球P静止于虚线X上方A点,在某一瞬间受到方向竖直向下、大小为I的冲量作用而做匀速直线运动.在A点右下方的磁场中有定点O,长为l的绝缘轻绳一端固定于O点,另一端连接不带电的质量同为m的小球Q,自然下垂.保持轻绳伸直,向右拉起Q,直到绳与竖直方向有一小于50的夹角,在P开始运动的同时自由释放Q,Q到达O点正下方W点时速率为v0.P、Q两小球在W点发生正碰,碰后电场、磁场消失,两小球粘在一起运动.P、Q两小球均视为质点,P小球的电荷量保持不变,绳不可伸长,不计空气阻力,重力加速度为g.