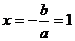|
直线名称 |
已知条件 |
直线方程 |
使用范围 |
示意图 |
|
点斜式 |
 |
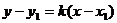 |
 |
|
|
斜截式 |
 |
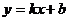 |
 |
|
|
两点式 |
 ( (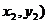 |
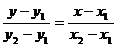 |
 |
|
|
截距式 |
 |
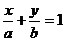 |
 |
|
设计意图:为帮助学生用联系的观点来学习知识,又能把四种形式的直线方程加以区别,以便更好地运用它们,本环节主要采用比较法的形式小结
 交
交 正半轴于AB两点,当
正半轴于AB两点,当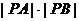 取到最小值时,求直线
取到最小值时,求直线
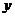 =0解得
=0解得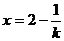 ;令
;令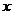 =0,解得
=0,解得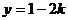
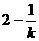 ,0),B(0,
,0),B(0,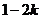 ),
),
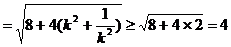
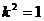 即
即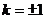 时,
时,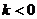 ,∴
,∴
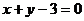
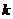 =1的情形
=1的情形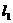 :
: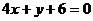 ,
, :
: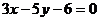 截得的线段的中点恰好是坐标原点,求该直线方程.
截得的线段的中点恰好是坐标原点,求该直线方程. ),则B点坐标为(
),则B点坐标为( )
) 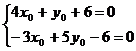
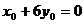 ,即点A在直线
,即点A在直线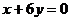 上,又直线
上,又直线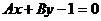 在
在 的倾斜角的2倍,则( )
的倾斜角的2倍,则( ) ,B=1 B.A=-
,B=1 B.A=-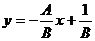 .
.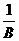 =-1,B=-1,故否定A、D.
=-1,B=-1,故否定A、D. =
=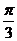 ,
, ,
, =-
=-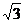 ,
, 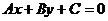 通过第二、三、四象限,则系数A、B、C需满足条件( )
通过第二、三、四象限,则系数A、B、C需满足条件( )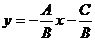 (B≠0)
(B≠0) <0,且-
<0,且- <0
<0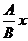 .
.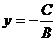 .由BC<0,得-
.由BC<0,得-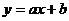 (
(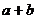 =0)的图象是( )
=0)的图象是( ) 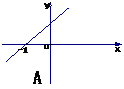


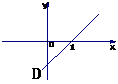
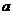 ,在
,在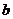
 .又因为
.又因为 ,∴
,∴