摘要:(1)过点P(2.1)作直线交正半轴于AB两点.当取到最小值时.求直线的方程. 解:设直线的方程为: 令=0解得,令=0.解得 ∴A(.0).B(0.). ∴= 当且仅当即时.取到最小值. 又根据题意.∴ 所以直线的方程为: 评述:此题在求解过程中运用了基本不等式.同时应注意结合直线与坐标轴正半轴相交而排除=1的情形 (2)一直线被两直线:.:截得的线段的中点恰好是坐标原点.求该直线方程. 解:设所求直线与.的交点分别是A.B.设A().则B点坐标为() 因为A.B分别在.上.所以 ①+②得:.即点A在直线上.又直线过原点.所以直线的方程为. (3)直线在轴上的截距是-1.而且它的倾斜角是直线的倾斜角的2倍.则( ) A. A=.B=1 B.A=-.B=-1 C.A=.B=-1 D.A=-.B=1 解:将直线方程化成斜截式. 因为=-1.B=-1.故否定A.D. 又直线的倾斜角=. ∴直线的倾斜角为2=. ∴斜率-=-. ∴A=-.B=-1.故选B (4)若直线通过第二.三.四象限.则系数A.B.C需满足条件( ) A.A.B.C同号 B.AC<0.BC<0 C.C=0.AB<0 D.A=0.BC<0 解法一:原方程可化为(B≠0) ∵直线通过第二.三.四象限. ∴其斜率小于0.轴上的截距小于0.即-<0.且-<0 ∴>0.且>0 即A.B同号.B.C同号.∴A.B.C同号.故选A 解法二: 若C=0.AB<0.则原方程化为=-. 由AB<0.可知->0. ∴此时直线经过原点.位于第一.三象限.故排除C. 若A=0.BC<0.则原方程化为.由BC<0.得->0. ∴此时直线与轴平行.位于轴上方.经过一.二象限.故排除D. 若AC<0.BC<0.知A.C异号.B.C异号 ∴A.B同号.即AB>0. ∴此时直线经过第一.二.四象限.故排除B.故A.B.C同号.应选A (5)直线(=0)的图象是( ) 解法一:由已知.直线的斜率为.在轴上的截距为 又因为=0. ∴与互为相反数.即直线的斜率及其在轴上的截距互为相反数 图A中.>0.>0;图B中.<0.<0;图C中.>0.=0 故排除A.B.C.选D. 解法二:由于所给直线方程是斜截式.所以其斜率≠0.于是令=0.解得.又因为=0.∴.∴ ∴直线在轴上的截距为1.由此可排除A.B.C.故选D
网址:http://m.1010jiajiao.com/timu_id_4448211[举报]
已知M(0,-2),点A在x轴上,点B在y轴的正半轴,点P在直线AB上,且满足
=
,
•
=0.
(1)当A点在x轴上移动时,求动点P的轨迹C的方程;
(2)过(-2,0)的直线l与轨迹C交于E、F两点,又过E、F作轨迹C的切线l1、l2,当l1⊥l2时,求直线l的方程. 查看习题详情和答案>>
| AP |
| PB |
| MA |
| AP |
(1)当A点在x轴上移动时,求动点P的轨迹C的方程;
(2)过(-2,0)的直线l与轨迹C交于E、F两点,又过E、F作轨迹C的切线l1、l2,当l1⊥l2时,求直线l的方程. 查看习题详情和答案>>
 =
= ,
,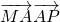 =0.
=0.